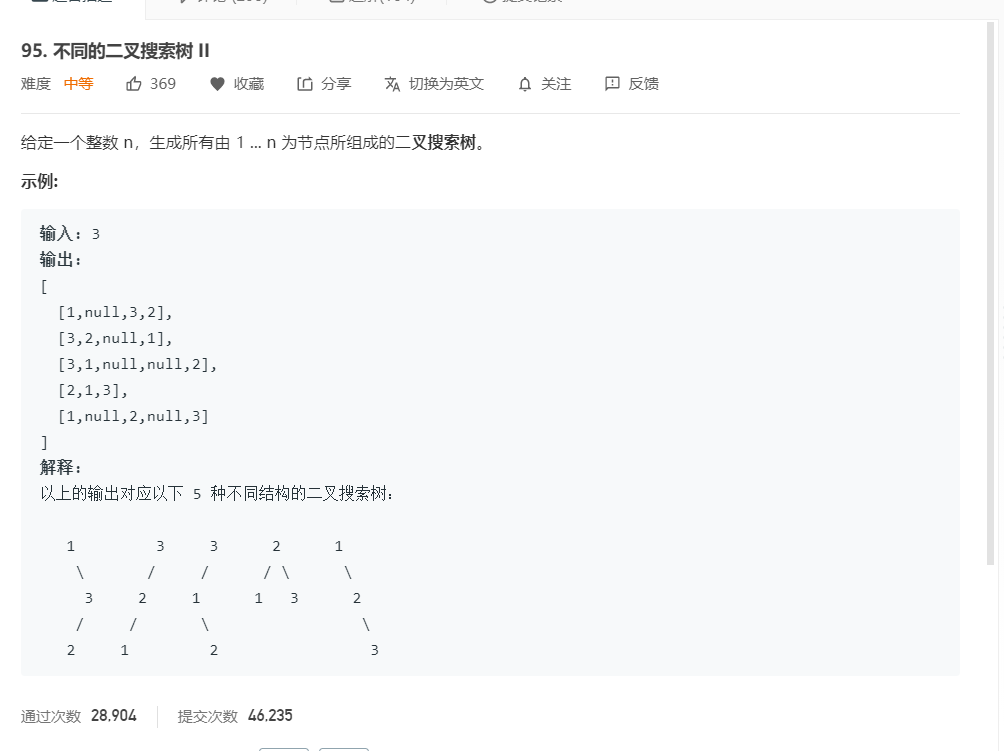
用递归即可
因为是二叉搜索树,也就是根大于左子节点,根小于右子节点,这就好办了,对于每个可能的根节点,求出所有左右子树的集合,双循环配对
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<TreeNode> generateTrees(int n) {
List<TreeNode> ans = new ArrayList<TreeNode>();
if (n == 0) {
return ans;
}
int start=1;
int end=n;
return getans(start,end);
}
public List<TreeNode> getans(int start,int end)//显然,结果里,只需要放二叉树的根就好
{
List<TreeNode> ans = new ArrayList<TreeNode>();//结果
if(start>end)//没有点,返回null
{
ans.add(null);
return ans;
}
if(start==end)//只有一个点,返回这个点为根节点的树就好
{
TreeNode T=new TreeNode(start);
ans.add(T);
return ans;
}
for(int i=start;i<=end;i++)//i是可能的根,所有循环,找的是所有的根
{
List<TreeNode> lefts=getans(start,i-1);//对于每个根,找所有可能的左右子树
List<TreeNode> rights=getans(i+1,end);
for (TreeNode leftTree : lefts) //双层循环,把以i为节点的,左子树,右子树结合为二叉搜索树,加到ans里面
for (TreeNode rightTree : rights)
{
TreeNode root=new TreeNode(i);//当前节点作为根节点
root.left=leftTree;
root.right=rightTree;
ans.add(root);//结果集合里面加上一个结果
}
}
return ans;
}
}