codeforces 939E Maximize! 双指针（two pointers）

E. Maximize!

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a multiset S consisting of positive integers (initially empty). There are two kind of queries:

1. Add a positive integer to S, the newly added integer is not less than any number in it.
2. Find a subset s of the set S such that the value 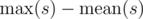 is maximum possible. Here max(s) means maximum value of elements in s,  — the average value of numbers in s. Output this maximum possible value of .

Input

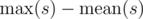The first line contains a single integer Q (1 ≤ Q ≤ 5·105) — the number of queries.

Each of the next Q lines contains a description of query. For queries of type 1 two integers 1 and x are given, where x (1 ≤ x ≤ 109) is a number that you should add to S. It's guaranteed that x is not less than any number in S. For queries of type 2, a single integer 2 is given.

It's guaranteed that the first query has type 1, i. e. S is not empty when a query of type 2 comes.

Output

Output the answer for each query of the second type in the order these queries are given in input. Each number should be printed in separate line.

Your answer is considered correct, if each of your answers has absolute or relative error not greater than 10 - 6.

Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if .

Examples

input

Copy

6
1 3
2
1 4
2
1 8
2

output

0.0000000000
0.5000000000
3.0000000000

input

Copy

4
1 1
1 4
1 5
2

output

2.0000000000


大意：一个多重集合（multiset，可以有重复元素的集合）刚开始为空，有两种操作：
1.加入一个数（保证加入的数大于等于集合中现有的数）
2.从multiset中选出一个子集，使得max-average最大，并输出。


YY：
1.由于插入元素的特殊性，这个多重集合用数组维护即可保证有序。
2.要使max-average最大，选出的子集大概是一个大哥带着一群小弟，而且这些小弟是从最小的开始且连续的。（一个较大的数和最小的几个数）

大概就是这样的————一个很大的数作为max，再选几个最小的数来拉低average。
3.如果选定一个max，以小弟的数量为自变量，max-average为因变量，这个函数是单峰的，使函数值最大的小弟数量称为“最佳小弟数量”。
4.对于选定的两个max，如果max1<max2，则  max2带着max1的小弟  一定比  max1带着自己的小弟 产生的答案（max-average）优，
而且如果max2带着比max1数量少的小弟  一定没有  max2带着max1的小弟 优。
所以选定最大值max2 取到最大max-average时，小弟数量一定大于等于 max1。


到这里，单调性非常明显，可以利用简洁的双指针法，一个变量pre代表小弟数量，maxx代表大哥是谁，sum代表当前累加和。
每加入一个数，算出以这个数为最大值时的最优解：
新的最大值带的小弟大于等于前一个最大值带的小弟，让新的最大值尝试带更多小弟，直到取到最大值（碰到了单峰函数的最大值）停止。

/*
Welcome Hacking
Wish You High Rating
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
using namespace std;
int read(){
    int xx=0,ff=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')ff=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){xx=xx*10+ch-'0';ch=getchar();}
    return xx*ff;
}
int Q;
int a[500010],cnt,maxx,pre,temp;
long long sum;
double ans;
int main(){
    //freopen("in","r",stdin);
    Q=read();
    while(Q--){
        if(read()==1){
            temp=read();
            a[++cnt]=temp;
            sum+=temp-maxx;
            maxx=temp;
            while(pre<cnt&&maxx-1.0*sum/(pre+1)<maxx-1.0*(sum+a[pre+1])/(pre+2))
                sum+=a[++pre];
            if(maxx-1.0*sum/(pre+1)>ans)
                ans=maxx-1.0*sum/(pre+1);
        }
        else
            printf("%.10f
",ans);
    }
    return 0;
}

ps：本题还可以利用单峰函数的性质，选定最大值，三分小弟数量。