非确定的自动机NFA确定化为DFA

摘要：

　在编译系统中，词法分析阶段是整个编译系统的基础。对于单词的识别，有限自动机FA是一种十分有效的工具。有限自动机由其映射f是否为单值而分为确定的有限自动机DFA和非确定的有限自动机NFA。在非确定的有限自动机NFA中，由于某些状态的转移需从若干个可能的后续状态中进行选择，故一个NFA对符号串的识别就必然是一个试探的过程。这种不确定性给识别过程带来的反复，无疑会影响到FA的工作效率。因此，对于一个非确定的有限自动机NFA M，经常的做法是构造一个确定的有限自动机DFA M’。

　有穷自动机（也称有限自动机）作为一种识别装置，能准确地识别正规集，即识别正规文法所定义的语言和正规式所表示的集合。引入有穷自动机理论，正是为词法分析程序的自动构造寻找特殊的方法和工具。
有穷自动机分为两类：确定的有穷自动机（Deterministic Finite Automata，DFA）和不确定的有穷自动机（Nondeterministic Finite Automata，NFA）。下面分别给出确定的有穷自动机和不确定的有穷自动机的定义、与其有关的概念、不确定的有穷自动机的确定化以及确定的有穷自动机的化简等算法。

　NFA转换为等价的DFA：在有穷自动机的理论里，有这样的定理：设L为一个由不确定的有穷自动机接受的集合，则存在一个接受L的确定的有穷自动机。这里不对定理进行证明，只介绍一种算法，将NFA转换成接受同样语言的DFA，这种算法称为子集法。宝阀为一个NFA构造相应的DFA的基本想法是让DFA的每一个状态对应NFA的一组状态。也就是让DFA使用它的状态去记录在NFA读入一个输入符号后可能达到的所有状态，在读入输入符号串a₁a₂...a_n，之后，DFA处在那样一个状态，该状态表示这个NFA的状态的一个子集T，T是从NFA的开始状态沿着某个标记为a₁a₂...a_n，的路径可以到达的那些状态构成的。

题目：

1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} )，其中 f(0,a)={0,1}  f(0,b)={0}  f(1,b)={2}  f(2,b)={3}

   画出状态转换矩阵,状态转换图，并说明该NFA识别的是什么样的语言。

	a	b
0	0,1	0
1		2
2		3
3

 

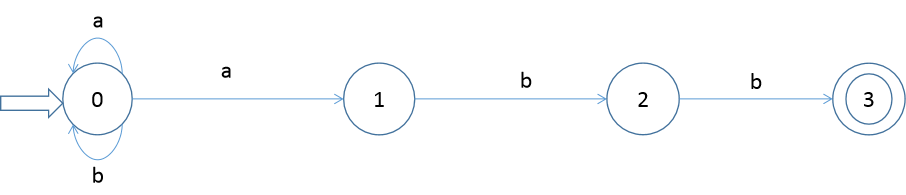
语言：(a | b)*abb

2.NFA 确定化为 DFA

1.解决多值映射：子集法

1）. 上述练习1的NFA

		a	b
A	{0}	{0,1}	{0}
B	{0,1}	{0,1}	{0,2}
C	{0,2}	{0,1}	{0,3}
D	{0,3}	{0,1}	{0}

DFA图：

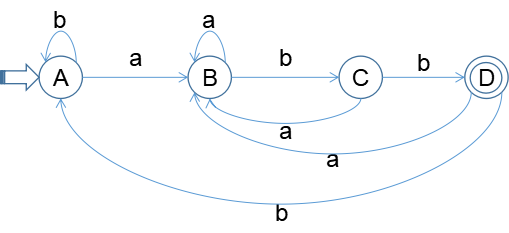
2）. P64页练习3

DFA状态转换矩阵

		0	1
A	{S}	{V,Q}	{Q,U}
B	{V,Q}	{Z,V}	{Q,U}
C	{Q,U}	{V}	{Q,U,Z}
D	{V}	{Z}
E	{Z,V}	{Z}	{Z}
F	{Q,U,Z}	{Z,V}	{Q,Z}
G	{Z}	{Z}	{Z}
H	{Q,Z}	{Z}	{Q,Z}

DFA图：

2.解决空弧：对初态和所有新状态求ε－闭包

1）. 发给大家的图2

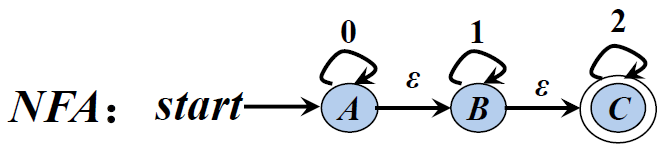
 DFA状态转换矩阵

		0	1	2
X	ε{A}={ABC}	ε{A}={ABC}	ε{B}={BC}	ε{C}={C}
Y	ε{BC}		ε{B}={BC}	ε{C}={C}
Z	ε{C}			ε{C}={C}

DFA图：

 

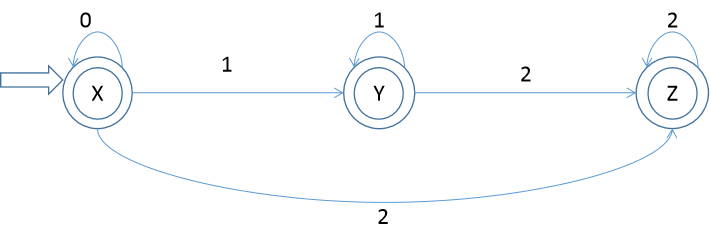
语法：(0*11* | 0*)22* 

2）.P50图3.6

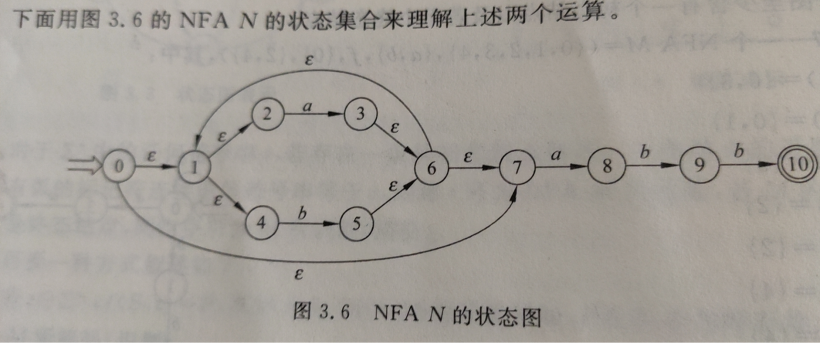
DFA状态转换矩阵

		a	b
0	ε{0}={01247}	ε{38}={3671248}	ε{5}={567124}
1	ε{1234678}	ε{38}={1234678}	ε{59}={5671249}
2	ε{124567}	ε{38}={3671248}	ε{5}={567124}
3	ε{1245679}	ε{38}={3671248}	ε{510}={56712410}
4	ε{12456710}	ε{38}={3671248}	ε{5}={567124}

DFA图：

子集法：

f(q,a)={q1,q2,…,qn},状态集的子集

将{q1,q2,…,qn}看做一个状态A，去记录NFA读入输入符号之后可能达到的所有状态的集合。

步骤：

1）.根据NFA构造DFA状态转换矩阵

①确定DFA的字母表，初态（NFA的所有初态集）

②从初态出发，经字母表到达的状态集看成一个新状态

③将新状态添加到DFA状态集

④重复23步骤，直到没有新的DFA状态

2）.画出DFA

3）.看NFA和DFA识别的符号串是否一致。