原文地址:https://zhuanlan.zhihu.com/p/84660707
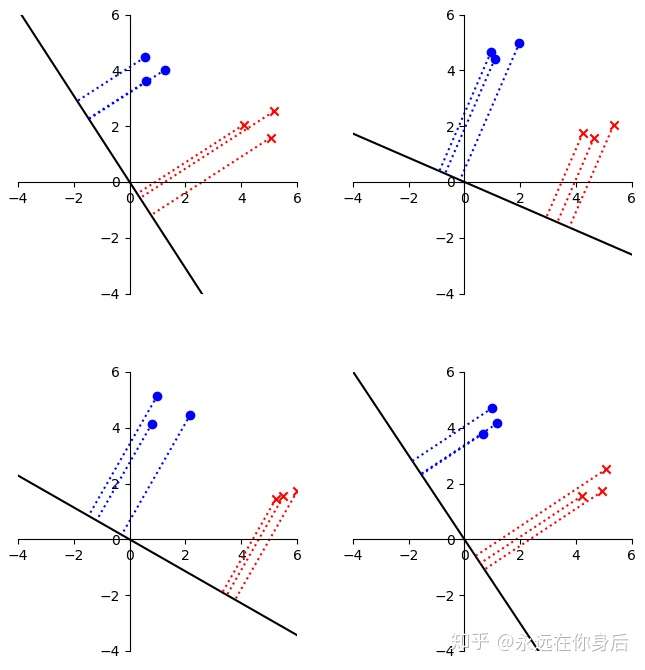
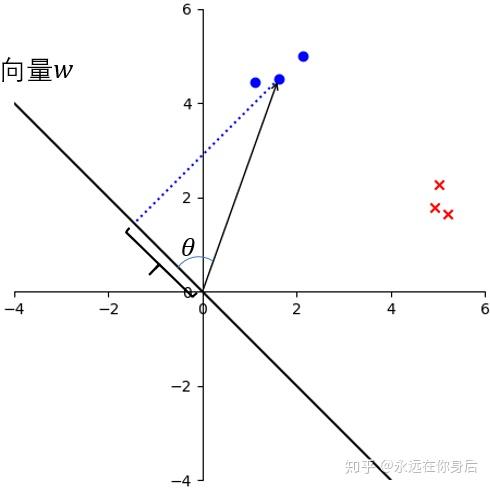
线性判别分析(Linear Discriminant Analysis, LDA),LDA是一种监督学习的降维技术,其具体的原理用一个栗子来说明。首先,从一个简单的分类开始,如下图所示
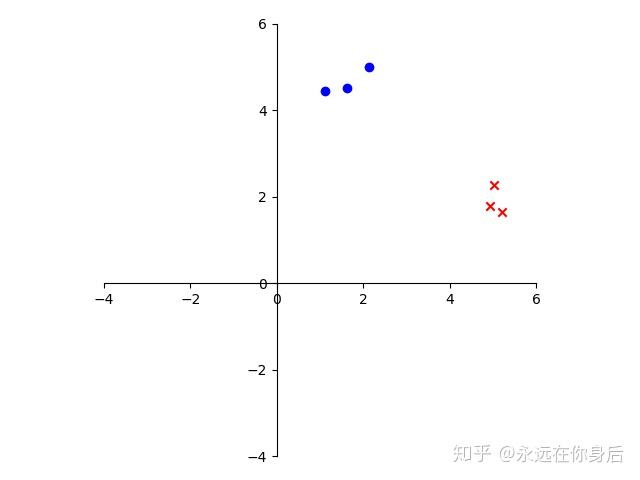
尝试找一个向量,并将各个样本投影到该向量上,比如
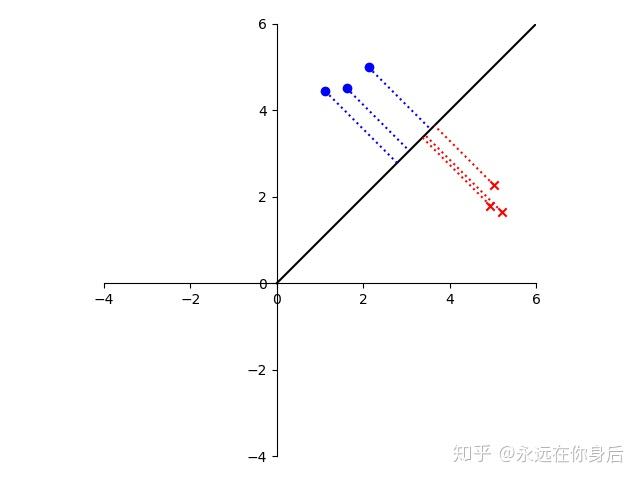
上面的向量虽然将两类样本区分开了,但是我们的目标并不是直接分开这两类样本,而是使它们的投影能够尽可能的分开,一个比较好的栗子如下所示:
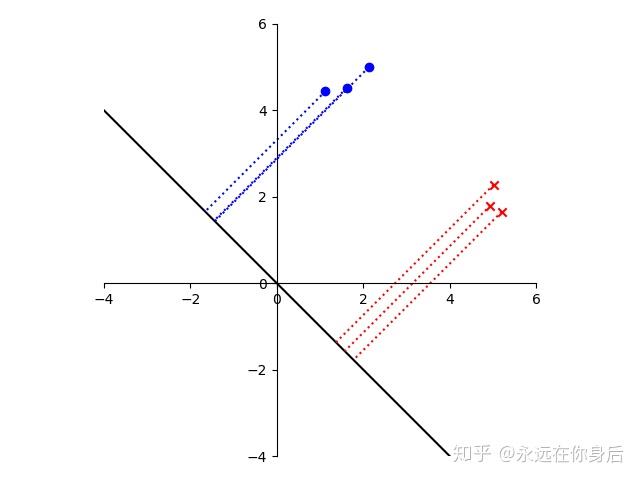
可以看到,投影后的结果,对于同一个类别的样本间隔很小,不同类别的样本间隔很大,这也正是LDA的目标,类内间隔小,类间间隔大。也许看到之后你会想到高内聚,低耦合
接着,来具体分析一下“投影”:
我们知道两个向量(例如 )的内积就是:
在
上的投影的模乘上
的模再乘上两者夹角的余弦
上图中 就是我们要找的向量,而且它是可以缩放的,所以我们令
,就能得到样本在
上的投影:
。并且,这是一个标量,于是再将上面的图像转一下,将
所在的直线当做一个数轴
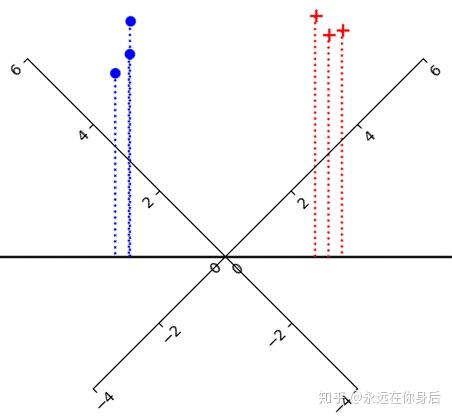
这样,一个样本投影到 上的结果就对应了该数轴上的一个值。现在,LDA的原理基本上清楚了,接着定义目标函数:
并求它的最大值(不是最小),而 的最优值就是
接下来看类间距离与类内距离的具体定义
- 类间距离
首先,投影得到一个标量
定义同一类样本投影后的均值
类间距离就可以定义为投影后均值之差的平方
到这一步,为了表达更方便,再定义某一类样本的均值
代入得到
- 类内距离
对于类内距离的衡量,一个很自然的想法就是使用方差
所有类内距离就是每个类的方差之和
上面的公式看起来比较多,但是这是因为写的比较详细的原因。接着令
代入得到
综合将类间距离和类内距离代入到 中,得到
其中 叫做类间散布矩阵,
叫做类内散布矩阵。不过还有一个问题就是这样会存在多个满足条件的
,所以需要进行约束,固定分母的值为1:
并求使分子值最大化的参数值,得到一个带约束的优化
因为这个优化带有约束,所以首先需要消除约束。令:
得到一个新的带约束优化目标
然后使用拉格朗日乘数法构造新的目标函数来统一 和
:
将 对
求导并使之等于0,得到
的最优值
观察上式标红部分, 是一个矩阵,是不是觉得很熟悉?显然
就是这个矩阵的特征向量。不过,这样还需要进行特征分解,我们可以将
拆开,得到
其中 是一个标量,也就是说
和
是共线的,这样,我们就可以求出
的方向了。到了这一步,就可以直接上代码了
class LDA(object):
def fit(self, positive, negative):
'''
positive, negative: 分别是正反样本的数据矩阵,列数相同,一行是一个样本
'''
# p_bar = positive.mean(axis=0, keepdims=True) # 求正例样本的平均
# n_bar = negative.mean(axis=0, keepdims=True) # 求反例样本的平局
# 计算类内散布矩阵
# p_tmp = positive - p_bar
# p_tmp = np.dot(p_tmp.T, p_tmp)
# n_tmp = negative - n_bar
# n_tmp = np.dot(n_tmp.T, n_tmp)
# S_w = p_tmp + n_tmp
# 根据Sw逆矩阵求解w
# w = np.dot(np.linalg.inv(S_w), np.transpose(p_bar-n_bar))
'''
其实Sw矩阵就是两类样本的协方差矩阵之和,所以代码可以进行简化
'''
S_w = np.cov(positive, rowvar=False) + np.cov(negative, rowvar=False)
w = np.dot(np.linalg.inv(S_w), np.mean(positive-negative, axis=0, keepdims=True).T)
return w最后,放几个随机生成数据的结果,看起来结果还是靠谱的