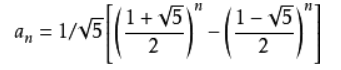- 斐波那契数列
- 前两项是1,从第三项开始是前两项的和
1,1,2,3,5,8.....
- 推导式
F(n) = F(n-1) + F(n-2)
F(0) = 1 F(1) = 1
- 最简单的斐波那契 (效率非常低)
- 时间复杂度为O(2的n次方)
def fibnacci(n): if n == 0 or n == 1: return 1 else: return fibnacci(n-1) + fibnacci(n-2)
- 斐波那契 1.0
- 时间复杂度O(n)
- 空间复杂度O(n)
def fib2(n): li = [1,1] for i in range(2, n+1): li.append(li[-1]+li[-2]) return li[n]
- 斐波那契2.0
- 时间复杂度O(n)
- 空间复杂度O(1)
def fib3(n): a = 1 b = 1 c = 1 for i in range(2, n+1): c = a + b a = b b = c return c
- 通项公式