第一章 模式识别基本概念
预习部分
首先了解了这门课涉及到了高等数学、线性代数、概率论等数学知识,所以我有稍微去粗略的回顾了一下这几门课的知识点。
复习部分
模式识别的应用领域有:字符识别(计算机视觉领域)、交通及标志识别(计算机视觉领域)、动作识别(计算机视觉领域)、语音识别(人机交互领域)、模式识别(医学领域)、应用程序识别(网络领域)、模式识别(金融领域)、股票价格预测(金融领域)、目标抓取(机器人领域)、无人驾驶(无人车领域)等。
模式识别分为“分类”和“回归”两种形式。模式是被本质上也是一种推理过程。
模型是一种关于已有知识的表达方式,即函数,它的组成:特征提取+回归器(狭义),特征提取+回归器+判别函数(广义)。分类器:回归器+判别函数。
特征向量:多个特征构成的列向量。
每个特征向量代表一个模式,度量特征向量两两之间的相关性是识别模式之间是否相似的基础。
点积可以表征两个特征向量的共线性,即方向的相似程度。点积为0则说明两个向量正交。两向量的夹角表示两个向量在方向上的差异性。
模型结构决定了模型有哪些参数。
线性模型适用于数据线性可分/线性表达的数据。非线性模型适用于数据线性不可分/线性不可表达的数据。(多项式、神经网络、决策树等)
N=M:参数有唯一解;N>>M:无准确解;N<<M:无数个解/无解。
机器学习方式:监督式学习(训练样本及输出真值给定)、无监督式学习(只给定训练样本,没给定输出真值)、半监督式学习、强化学习。
泛化能力:学习算法对新模式的决策能力。
过拟合:泛化能力差的表现(训练阶段表现很好,测试阶段表现很差)。
提高泛化能力的思路:不要过度训练。
1.选择复杂度适合的模型。
2.在目标函数中加入正则项。(正则化)
评估方法:留出法、K折交叉验证、留一验证。
性能指标:
1.二类分类:真阳性(TP)、假阳性(FP)、真阴性(TN)、假阴性(FN)。
2.多类分类:依次以单个类作为正类,其余为负类。
准确性、精度、召回率。
PR曲线:横轴为召回率,纵轴为精度。曲线越往上凸,则性能越好。对各类别之间样本分布比例敏感。
ROC曲线:横轴为FPR,纵轴为TPR。曲线越往左上凸,则性能越好。对各类别之间样本分布比例不敏感。
曲线下方面积AUC=1:完美分类器;0.5<AUC<1:优于随机猜测;AUC=0.5:跟随机猜测一样;AUC<0.5:比随机猜测差。
第二章 基于距离的分类器
预习部分
我提前了解了这一章是基本是关于分类器的,所以就先去了解了一下哪几种常见的分类器的概念及应用。
复习部分
(以下我是把分类器都放到了一起总结的)
MED分类器是基于欧式距离的分类器
欧式距离 d(x1,x2)=(x2−x1)T∗(x2−x1)。
判别方法: (x−μ1)T(x−μ1)<(x−μ2)T(x−μ2)?C1类:C2类。
受特征的量纲、分布不同的影响,易导致分类错误,一般不直接用欧式距离进行分类
MICD分类器是基于马氏距离的分类器
马氏距离 d(x1,x2)=(x2−x1)TΣ−1x(x2−x1)
判别方法:(x−μ1)TΣ−1x(x−μ1)<(x−μ2)TΣ−1x(x−μ2)?C1类:C2类
针对欧式距离出现的问题,对特征进行解耦与白化,转化后的点间距离为马氏距离
消除了特征间的相关性并使特征具有相同方差,从而使其不受量纲和分布的影响,提高分类准确度
但在距离相等时,倾向于归于方差较大的类
特征白化:将原始特征映射到一个新的空间,是的新空间中特征的协方差矩阵为单位矩阵,从而去除特征变化的不同及特征之间的相关性。
特征转换:先解耦再白化。
MAP分类器是基于后验概率的分类器
后验概率 p(Ci|x)=p(x|Ci)p(Ci)p(x)
判别方法:p(x|C1)p(C1)>p(x|C2)p(C2)?C1类:C2类
选择后验概率最大的类作为判别结果,即最小化概率误差
贝叶斯分类器基于MAP分类器
判别方法:R(αi|x)<R(αj|x)?Ci类:Cj类
KNN分类器是基于MAP分类器,但假设观测似然概率基于KNN估计
由KNN估计,p(x|Ci)=kiNiV,p(x)=kNV
又p(Ci)=NiN。故p(Ci|x)=p(x|Ci)p(Ci)/p(x)=kik
对于测试样本x,我们找到与其距离最近的k个样本,其中哪个类别的样本最多,就将x归于那一类。即选择最大的ki,使得后验概率最大。
第三章 贝叶斯决策和学习
预习部分
这章主要是讲贝叶斯决策,所以我就事先先在网上查阅了一些关于贝叶斯的相关知识,再加上上学期的人工智能有稍微讲到贝叶斯,所以我对贝叶斯就有了一个初步的认识了。
复习部分
(分类器我在第二章有讲到,所以这里关于分类器的东西都不讲了)
单维高斯分布:
高斯观测概率

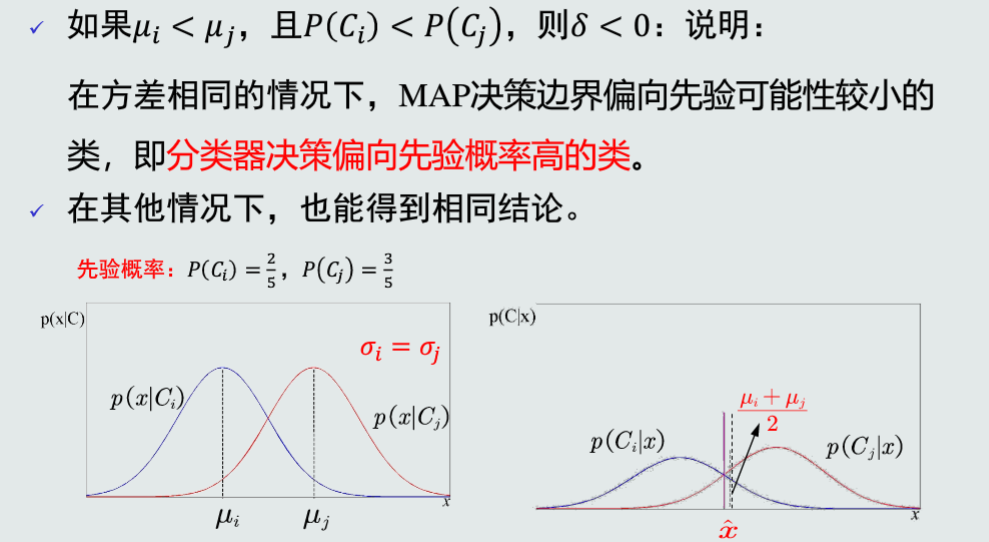
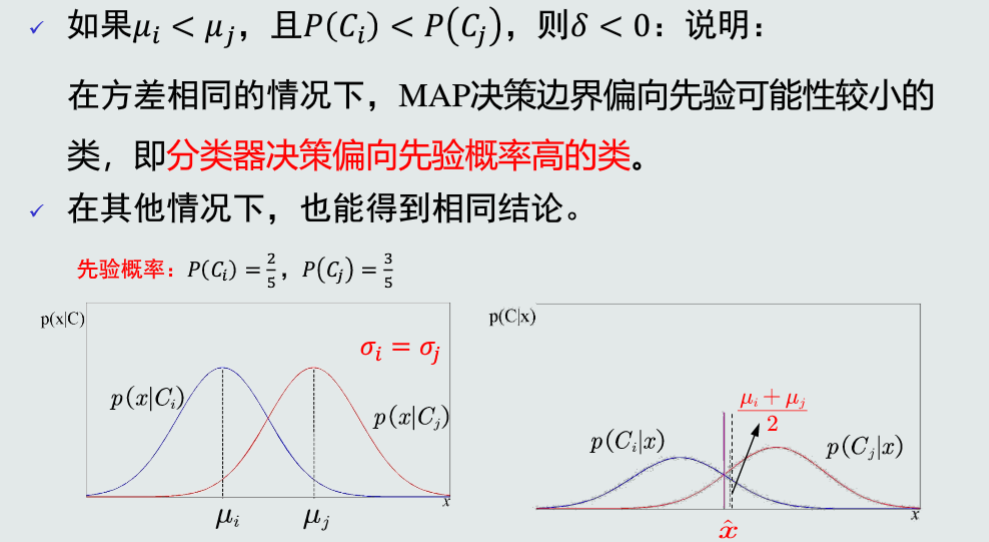

所以MAP分类器可以解决MICD分类器存在的问题:方差不同时,MAP分类器倾向于方差小的类。
MAP、MICD、MED分类器的比较:

决策风险:
贝叶斯分类器的决策目标:最小化期望损失
朴素贝叶斯分类器:
拒绝选项: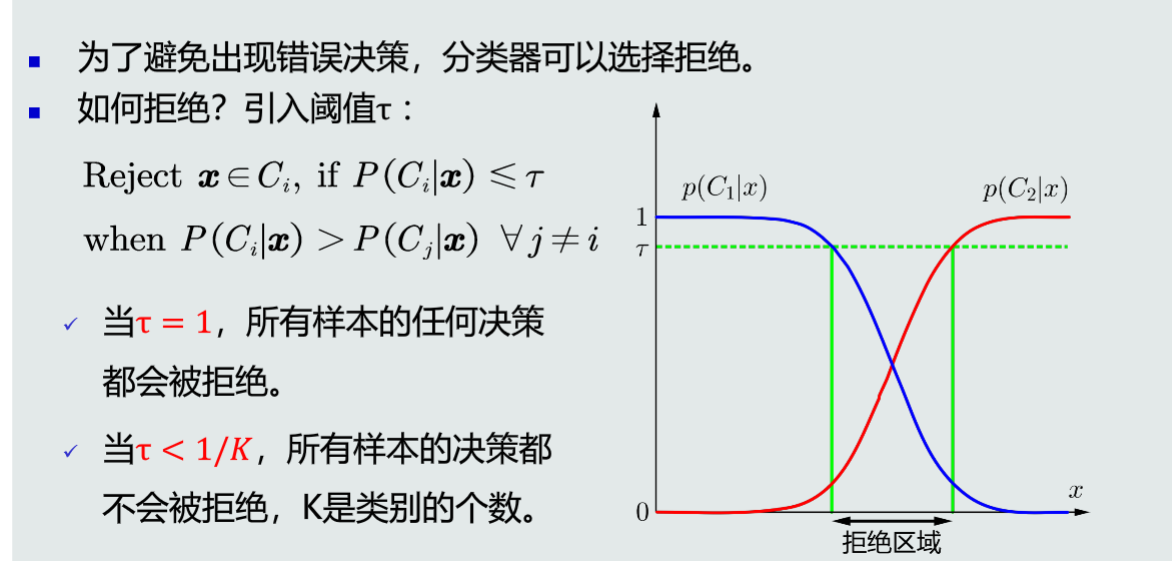
监督式学习方法:1.参数化方法。(最大似然估计、贝叶斯估计)2.非参数化方法。
无偏估计:一个参数的估计量的数学期望是该参数的真值。意味着只要训练样本个数足够多,该估计值就是参数的真实值。
均值的最大似然估计是无偏估计。
协方差的最大似然估计是有偏估计。
贝叶斯估计:给定参数分布的先验概率以及训练样本,估计参数分布的后验概率。




无参数技术:K近邻法、直方图技术、核密度估计。
直方图估计的优缺点:
核密度估计的优缺点:
第四章 线性判据与回归
预习部分
事先看了一下这章的大概内容,了解了梯度下降法,而且对这种方法很感兴趣,觉得他就很像高数中用导数求函数的最值一样,一般用导数算出来的都是极值,但极值也不一定是最值,这就跟梯度下降法的局部最优跟全局最优一样。
复习部分
生成模型的优劣势:


判别模型的优势: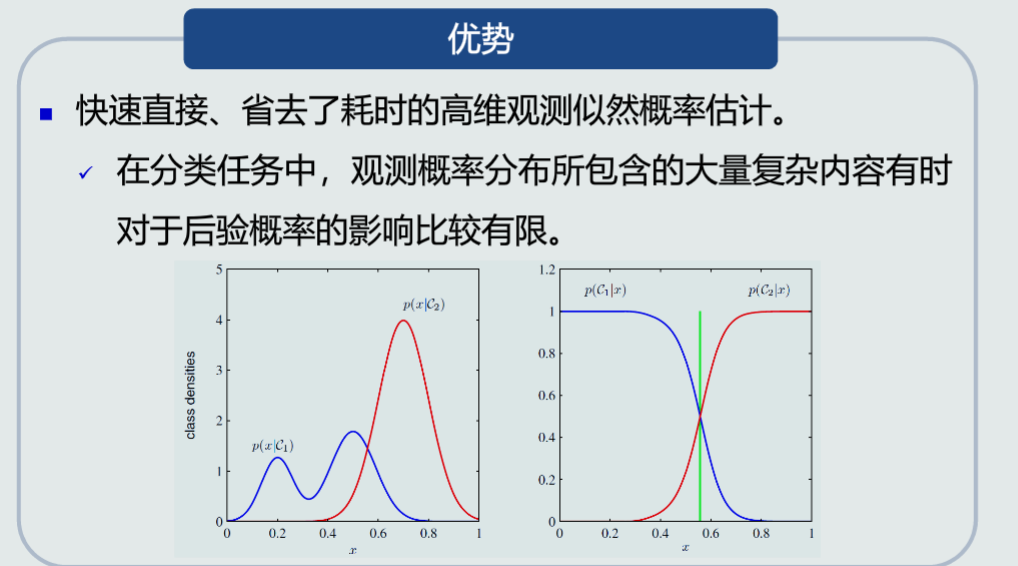
线性判据优势:计算量少,适用于训练样本少的情况
寻找最优解:1.设计目标函数。2.加入约束条件。
并行感知机的思想:被错误分类的样本最少。
梯度下降法:使用当前梯度值迭代更新参数。通常加入步长来调整更新的幅度。
串行感知机的思想:当前样本被错误分类的程度最小。
步长决定收敛速度、以及是否收敛到局部或者全局最优点。
提高感知机的泛化能力:加入Margin约束
Fisher线性判据:

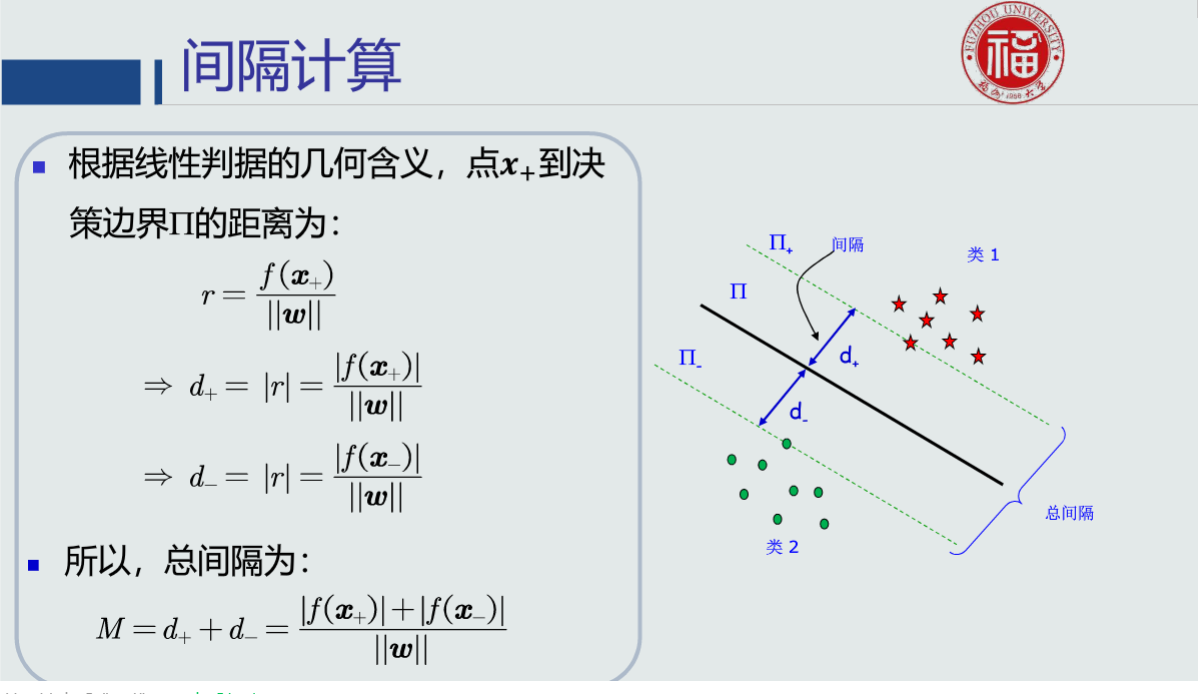
支持向量机(SVM)的目标:最大化总间隔。
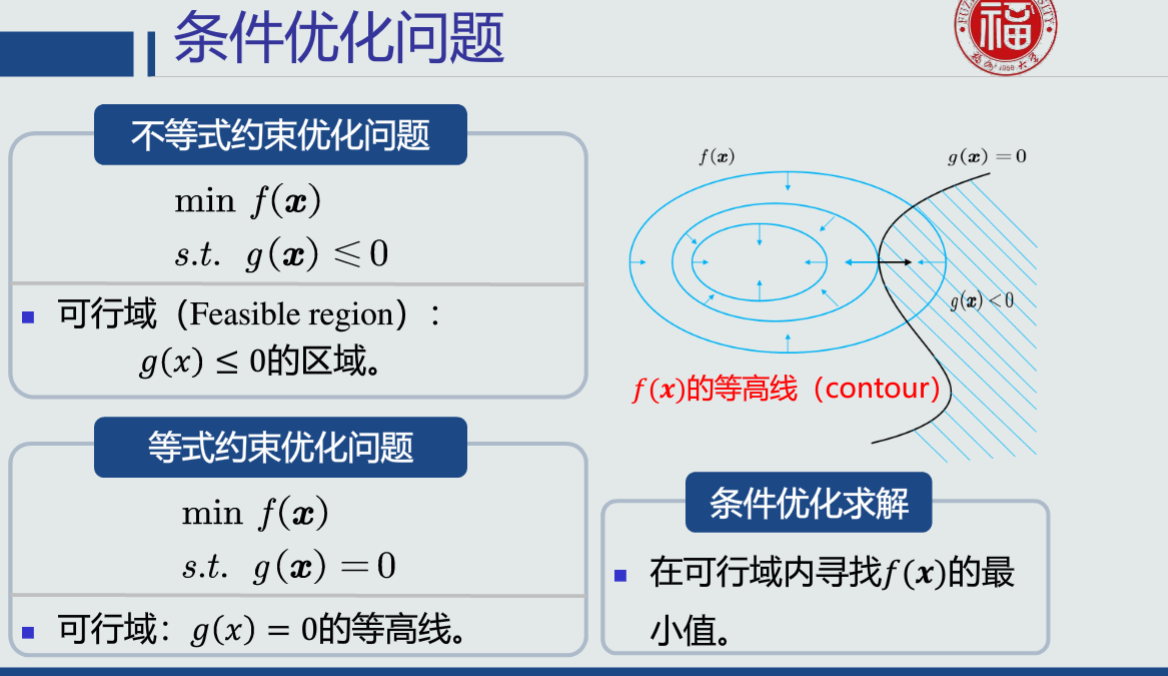
支持向量机的目标函数是一个条件优化问题。常用拉格朗日乘数法。
学习心得
学习心得就是累。太难了,公式好多好复杂啊,而且有的推导过程也看不懂。