0.PTA得分截图

1.本周学习总结(5分)
1.1 绪论(1分)
1.1.1 数据结构有哪些结构,各种结构解决什么问题?
1)逻辑结构
- 线性结构
- 树形结构
- 图形结构
2)存储结构
- 数组(顺序存储)
- 链表(链式存储)
(1)数组的元素个数是固定的,而组成链表的结点个数可按需要增减;
(2)数组元素的存诸单元在数组定义时分配,链表结点的存储单元在程序执行时动态向系统申请;
(3)数组中的元素顺序关系由元素在数组中的位置(即下标)确定,链表中的结点顺序关系由结点所包含的指针来体现;
(4)对于不是固定长度的列表,用可能最大长度的数组来描述,会浪费许多内存空间;
(5)对于元素的插人、删除操作非常频繁的列表处理场合,用数组表示列表也是不适宜的。若用链表实现,会使程序结构清晰,处理的方法也较为简便。
1.1.2 时间复杂度及空间复杂度概念。
- 算法的时间复杂度,用来度量算法的运行时间,记作: T(n) = O(f(n))。它表示随着 输入大小n 的增大,算法执行需要的时间的增长速度可以用 f(n) 来描述。
- 算法的空间复杂度,是对一个算法在运行过程中临时占用存储空间的度量,一个算法在计算机存储器上所占用的存储空间包括存储算法本身所占用的空间,算数和输入输出所占用的存储空间以及临时占用存储空间三个部分,算法的输入输出数据所占用的存储空间是由待解决的问题来决定的,通过参数表由调用函数而来,它随本算法的不同而改变,存储算法本身所占用的存储空间有算法的书写长短成正比。算法在运行过程中占用的临时空间由不同的算法决定。
1.1.3 时间复杂度有哪些?如何计算程序的时间复杂度和空间复杂度,举例说明。
常数阶O(1),对数阶O(),线性阶O(n),线性对数阶O(nlog2n),平方阶O(n2),立方阶O(n3),k次方阶O(nk),指数阶O(2n)
- 时间复杂度
void fun(int n) {
int i = l;
while (i <= n)
i = i * 2;
}
基本运算是i=i*2
设其执行时间为T(n)
所以2T(n)<=n
即T(n)<=log2n=O(log2n)。
- 空间复杂度
for(int i = 0 ; i <n; i ++){
for(int j = i ; j< n ; j++){
int k = 0;
}
}
一共两层循环
所以S(n)=O(n²)。
1.2 线性表(1分)
1.2.1 顺序表
线性表的顺序存储结构是把线性表中的所有元素按照其逻辑顺序依次存储到从计算机存储器中指定存储位置开始的一块连续的存储空间中,线性表中逻辑上相邻的两个元素在对应的顺序表中的存储位置也相邻。
- 初始化顺序表
List InitList()
{
List L;
L = new SqList;////分配存放顺序表的空间
L->Last = 0;
returnL;
}
}
- 建立顺序表
void MakeList(List& L)
{
int i;
cin >> n;
for (i = 0; i < n; i++)
{
cin >> L->Data[i]; //输入数据
}
L->Last = n; //设置表长
}
- 销毁顺序表
void DestroyList(List &L)
{
delete L;
}
- 插入数据
bool Insert(List L, ElementType e, Position P)
{
int i;
if (L->Last + 1 >= MAXSIZE) //判断空间是否已满
{
return false;
}
if (P > (L->Last + 1) || P < 0) //参数错误时返回false
{
return false;
}
for (i = L->Last; i >= P; i--) //将data[P]及后面元素后移一个位置
{
L->Data[i + 1] = L->Data[i];
}
L->Data[P] = X; //插入数据
L->Last += 1; //顺序表长度加1
return true;
}
- 删除数据
bool Delete(List L, Position P)
{
int i;
if (P > L->Last || P < 0)
{
return false; //参数错误返回 false
}
for (i = P; i < L->Last; i++)
{
L->Data[i] = L->Data[i + 1]; //将data[P]之后的元素向前移动一个位置
}
L->Last -= 1; //顺序表长度减1
return true;
}
1.2.2 链表(2分)

- 遍历链表、p->next、p->data前要考虑吧p是否为空。
- 链表重构前要保护原有链的关系。(p=L->next; L->next=NULL;)
- 链表插入时,注意插入点的前驱指针在哪(通过pre->next获取)。
- 设计一个新指针来保留后继。(q=p; p=p->next;)
顺序表:
- 顺序表存储是将数据元素放到一块连续的内存存储空间,相邻数据元素的存放地址也相邻(逻辑与物理统一)。
- 空间利用率高(局部性原理,连续存放,命中率高);存取速度高效,通过下标来直接存储。
- 但是插入和删除比较慢,比如:插入或者删除一个元素时,整个表需要遍历移动元素来重新排一次顺序;不可以增长长度,有空间限制,当需要存取的元素个数可能多于顺序表的元素个数时,会出现"溢出"问题.当元素个数远少于预先分配的空间时,空间浪费巨大。
链表:
- 单链表是只包含指向下一个节点的指针,只能单向遍历。双链表即包含指向下一个节点的指针,也包含指向前一个节点的指针,因此可以双向遍历。循环单链表则是将尾节点与首节点链接起来,形成了一个环状结构。
- 存取某个元素速度慢;插入和删除速度快,保留原有的物理顺序,比如:插入或者删除一个元素时,只需要改变指针指向即可;没有空间限制,存储元素的个数无上限,基本只与内存空间大小有关.。
- 但是占用额外的空间以存储指针(浪费空间,不连续存放) ;查找速度慢,因为查找时,需要循环链表访问,需要从开始节点一个一个节点去查找元素访问。
头插法建立单链表:
void CreateListF(LinkList& L, int n)
{
LinkList head, ptr;
head = new(LNode); //创建头结点
head->next = NULL; //初始化头结点的后继为NULL
for (int i = 0; i < n; i++)
{
ptr = new(LNode); //创建新结点
cin >> ptr->data;
ptr->next = head->next; //连接表身
head->next = ptr; //将新结点插到表头
}
L = head;
}
头插法建立双链表:
void CreataListF(DLinkNode*& L, ElemType a[], int n)
{
DLinkNode* s;int i;
L = (DLinkNode*)malloc(szeof(DLinkNode));//创建头结点
L->prior = L->next = NULL;//前后指针域置为NULL
for(i = 0;i < n;i++)
{
s = (DLinkNode*)malloc(sizeof(DLinkNode));
s->data == a[i];
s->next = L->next;//将*s插入到头结点之后
if (L->next != NULL)//若L存在数据结点,修改前驱指针
L->next->prior = s;
L->next = s;
s->prior = L;
}
}
(开始时的首结点需要为空,否则后面插入的最后指向不明,并且需要申请新的结点来存放数据,再通过改变指向来实现头插法)
尾插法建立单链表:
void CreateListR(LinkList& L, int n)
{
LinkList ptr, head, tail;
head = new LNode; //创建头结点
tail = head; //尾结点指向表尾,初始化为头结点
head->next = NULL; //头结点的后继初始化为NULL
for (int i = 0; i < n; i++)
{
ptr = new LNode; //创建新结点
cin >> ptr->data
ptr->next = NULL;
tail->next = ptr; //新结点插在表尾
tail = ptr; //更新表尾
}
L = head;
}
尾插法建立双链表:
void CreataListR(DLinkNode*& L, ElemType a[], int n)
{
DLinkNode* s,*r;
int i;
L = (DLinkNode*)malloc(szeof(DLinkNode));//创建头结点
L->prior = L->next = NULL;//前后指针域置为NULL
r = L;
for(i = 0;i < n;i++)
{
s = (DLinkNode*)malloc(sizeof(DLinkNode));
s->data == a[i];//创建数据节点*s
r->next = s;
s->prior = r;//将*s*r之后
r = s;//r指向尾结点
}
r->next = NULL;
}
(结尾要添上NULL的标志)
链表操作注意事项:
(1)遍历链表的时候要考虑指针是否为空,要考虑是p->next还是p。
(2)链表删除注意链表是否为空,以及删除结点的查找。
(3)链表插入注意插入的结点判断,采取合适的插法。
(4)有时需要新建结点来保留指针,实现分离分开的操作。
(5)新建结点若明确指向已存在的链表则不需要再申请,若作为临时保留则需要申请内存。
链表及顺序表在存储空间、插入及删除操作方面区别,优势?
顺序表的空间存储利用率高,空间存储有限,考虑溢出问题,存取速率快。但实现数据的插入和删除则需要较多的时间。
链表没有空间限制,其插入和删除的速率也较快,但是存取和查找的较耗时。
1.2.3 有序表及单循环链表(1分)
- 有序顺序表插入:
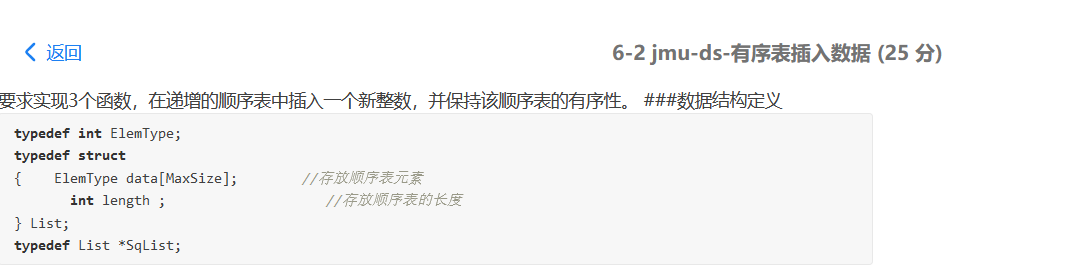
bool ListInsert(SqList*& L, int i, ElemType e)
{
int j;
if (i<1 || i>L->length + 1)
return false;
i--;
for (j = L->length;j > i;j--)
L->data[j] = L->data[j - 1];
L->data[i] = e;
L->length++;
return true;
}
- 有序单链表数据插入、删除:

bool ListInsert(LinkNode*& L, int i, ElemType e)//链表插入数据
{
int j = 0;
LinkNode* p = L, * s;
if (i <= 0) return false;
while (j < i - 1 && p != NULL)//查找第i-1个结点p
{
j++;
p = p->next;
}
if (p == NULL)
return false;
else//找到结点,插入新结点并返回true
{
s = (LinkNode*)malloc(sizeof(LinkNode));
s->data = e;//创建新结点s,其data域置为e
s->next = p->next;//讲s结点插入到p之后
p->next = s;
return true;
}
}
bool ListDelete(LinkNode*& L, int i, ElemType& e)//链表删除数据
{
int j = 0;
LinkNode* p = L, * q;
if (i <= 0) reutrn false;
while (j < i - 1 && p != NULL)
{
j++;
p = p->next;
}
if (p == NULL)
return false;
else
{
q = p->next;
if (q == NULL)
return false;
e = q->data;
p->next = q->next;//从单链表中删除q结点
free(q);//释放q结点
return true;
}
}
- 有序链表合并:
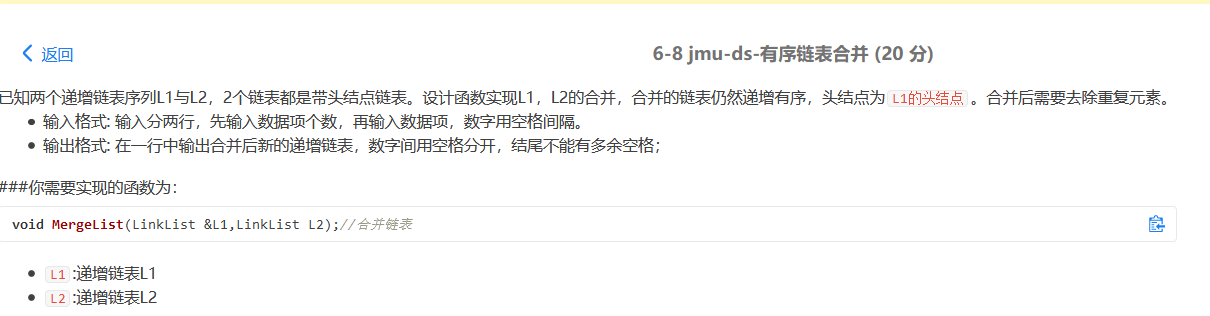
void MergeList(LinkList& L1, LinkList L2)//合并链表
{
LinkList L, ptr = L1;
while (ptr->next && L2->next)
{
if (ptr->next->data > L2->next->data)
{
L = new LNode;
L->next = ptr->next;
L->data = L2->next->data;
ptr->next = L;
L2 = L2->next;
}
else
if (ptr->next->data == L2->next->data)
L2 = L2->next;
ptr = ptr->next;
if (ptr->next == NULL && L2->next != NULL)
ptr->next = L2->next;
}
}
单循环链表特点,循环遍历方式?
循环链表的特点是无须增加存储量,仅对表的链接方式稍作改变,即可使得表处理更加方便灵活。表中尾结点的指针改为指向表头结点,整个链表形成一个环,从表中任一结点出发都可以找到链表中其他的结点。
3. PTA实验作业(4分)
3.1 两个有序序列的中位数

3.1.1解题思路及伪代码
- 思路:
创建一个新链表并输入第一个序列,再将第二个序列的元素作为temp依次与链表中的元素作比较后插入到链表中,最后计算出链表中间的两位数据的平均数即为中位数medain - 伪代码:
typedef struct LNode
{
int data;
struct LNode* next;
}LNode, * LinkList; //数据结构定义
For (int i = 1;i <= n;i++) 输入第一序列的数
For (int i = 1;i <= n;i++) 输入temp(第二序列的数)
while (ptr->next != NULL && ptr->next->data < temp) 继续比较下一个数据
直至比较到ptr->next == NULL
For (int i = 1;i <= n;i++) L = L->next;
并 median = (L->data + L->next->data) / 2;
Cout <<median;
3.1.2 总结解题所用的知识点
- 有序链表的插入
3.2 一元多项式的乘法与加法运算
3.2.1 解题思路及伪代码
- 思路:
1. 创建多项式
2. 多项式相加
3. 输出链表
4. 销毁链表
*因为是降序排列,所以多项式相加时需要采用头插法 - 伪代码:
比较指数大小,相同系数的指数合并
while(t1和t2)
t1>t2
t2>t1
t1==t2
3.2.2 总结解题所用的知识点
- 建立链表
- 链表的合并
- 尾插法
4.阅读代码(1分)
4.1 题目及解题代码
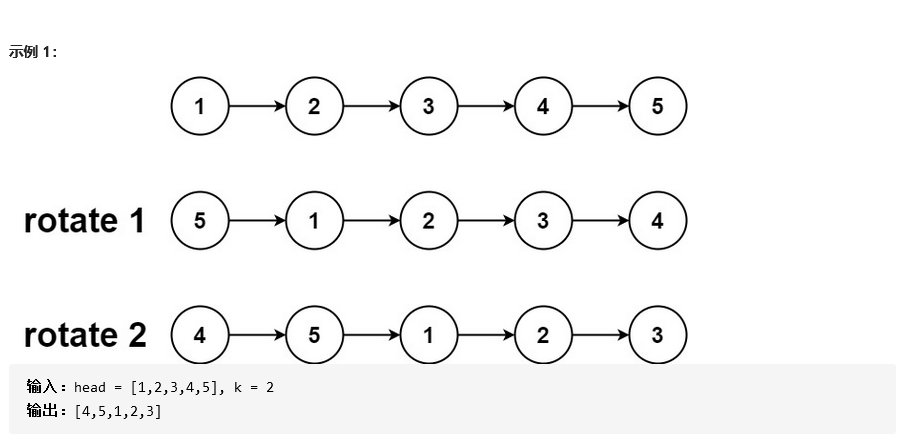
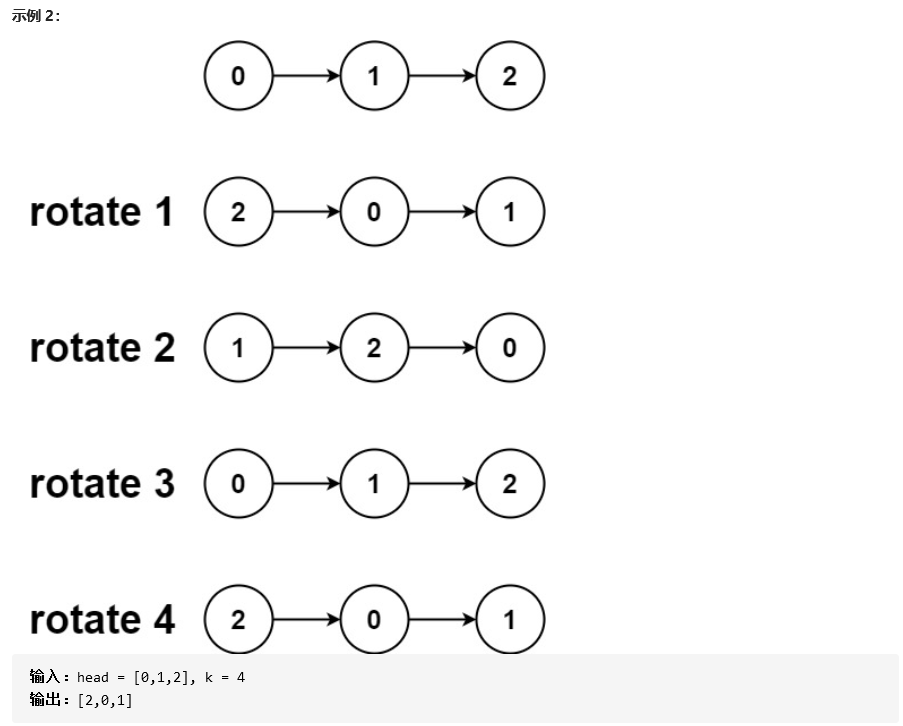
61. 旋转链表

代码:
struct ListNode* rotateRight(struct ListNode* head, int k) {
if (k == 0 || head == NULL || head->next == NULL) {
return head;
}
int n = 1;
struct ListNode* iter = head;
while (iter->next != NULL) {
iter = iter->next;
n++;
}
int add = n - k % n;
if (add == n) {
return head;
}
iter->next = head;
while (add--) {
iter = iter->next;
}
struct ListNode* ret = iter->next;
iter->next = NULL;
return ret;
}
4.2 该题的设计思路及伪代码
记给定链表的长度为n,注意到当向右移动的次数k≥n时,我们仅需要向右移动k mod n次即可(因为每n次移动都会让链表变为原状)
新链表的最后一个节点为原链表的第(n−1)−(k mod n)个节点(从0开始计数)
先将给定的链表连接成环,然后将指定位置断开
首先计算出链表的长度n,并找到该链表的末尾节点,将其与头节点相连。这样就得到了闭合为环的链表
找到新链表的最后一个节点(即原链表的第(n−1)−(k mod n)个节点),将当前闭合为环的链表断开,即可得到我们所需要的结果
- 时间复杂度:O(n),最坏情况下,需要遍历该链表两次。
- 空间复杂度:O(1),只需要常数的空间存储若干变量。
4.3 分析该题目解题优势及难点。
- 当链表长度不大于1,或者k为n的倍数时,新链表将与原链表相同,我们无需进行任何处理