0.PTA得分截图

1.本周学习总结
1.1栈
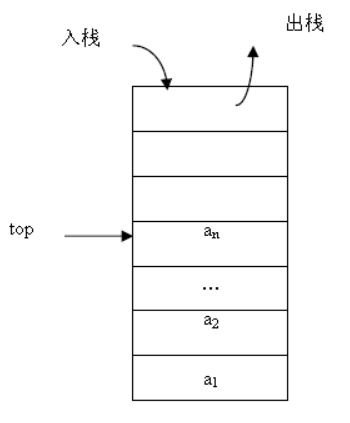
- 栈:允许在同一端进行插入和删除操作的特殊线性表。允许进行插入和删除操作的一端称为栈顶(top),另一端为栈底(bottom);栈底固定,而栈顶浮动;栈中元素个数为零时称为空栈。插入一般称为进栈(PUSH),删除则称为退栈(POP)。栈也称为先进后出表。
- 当栈中没有数据元素时称为空栈。
- 栈的插入操作称为入栈或者进栈,栈的删除操作称为出栈或者退栈。
- 栈的主要特点为后进先出,每次出栈的元素都为当前栈的栈顶元素。
1.1.1顺序栈
- 顺序栈的结构体定义:
#define MAXSIZE 20
typedef int ElemType;
typedef struct
{
ElemType data[MAXSIZE];//存放元素
int top = -1; //用于栈顶指针,下标
}SqStack;//顺序栈的类型
- 初始化栈:
void InitStack(SqStack &s)
{
s=new SqStack;//动态申请内存
s->top=-1;
}
- 是否为空栈:
bool IsEmpty(SqStack s)//如果为空返回true,不为空则返回false;
{
if(s.top==-1)
return true;
else
return false;
}
- 进栈:
bool Push(SqStack &S,ElemType e)
{
if(s->top==MaxSize-1)//顺序栈进栈时要注意栈是否已满
{
return false;
}
s->top++;//栈顶指针加1
s->data[s->top]=e;
return true;
}
- 出栈:
bool Pop(SqStack &s,ElemType &e)
{
if(s->top==-1)//顺序栈出栈时要注意栈是否为空
{
return flase
}
e=s->data[s->top];
s->top--;//栈顶指针减一
return ture;
}
- 取栈顶元素:
bool GetTop(SqStack *s,ElemType &e)
{
if(s->top==-1)//判断是否为空
return false;
e=s->data[s->top];
return true;
}
- 销毁栈:
void DestroyStack(SNode &s)
{
delete s;
}
1.1.2链栈

- 链栈的结构体定义:
typedef struct linknode
{
ElemType data;//数据域
struct linknode *next;//指针域
}LinkStNode;//链栈类型
- 初始化栈:
void InitStack(LiStack &s)
{
s=new LiNode;//动态申请内存
s->next=NULL;
}
- 进栈:
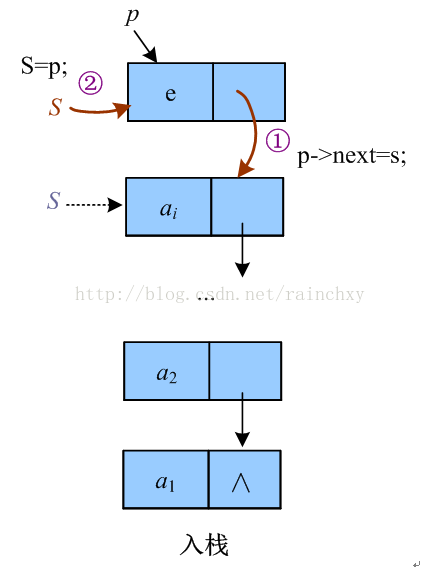
void Push(LiStack &s,Elemtype e)
{
LiStack p;
p=new LiNode;//新建结点进行插入
p->data=e;//头插法
p->next=s->next;
s->next=p;
}
- 出栈:
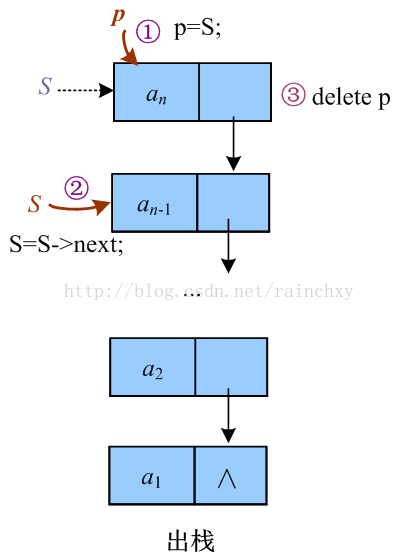
bool Pop(LiStack &s,ElemType &e)
{
LiStack p;//新建结点临时保存
if(s->next=NULL)
{
return false;
}
p=s->next;
e=p->data;
s->enxt=p->next;//改变结点指向
delete p;//删除
return true;
}
- 取栈顶元素:
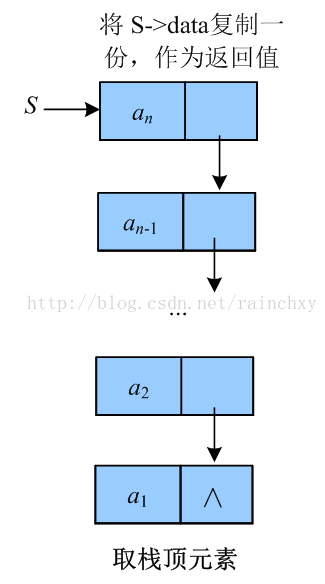
int GetTop(LinkStack S) //返回S的栈顶元素,不修改栈顶指针
{
if (S != NULL) //栈非空
return S->data; //返回栈顶元素的值,栈顶指针不变
else
return -1;
}
1.1.3 C++类模板:stack
#include <stack>
stack <Elemtype> s;初始化栈,保存Elemtype类型的数据;
s.push(x);入栈元素t;
s.top();返回栈顶指针;
s.pop();出栈操作,只做删除栈顶元素的操作,不返回该删除元素;
s.empty();判断是否栈空,如果为空返回true;
s.size();返回栈中元素个数;
1.2 栈的应用
简单表达式求值
将算术表达式转换成后缀表达式
在将一个中缀表达式转换成后缀表达式时,操作数之间的相对次序是不变的,但运算符的相对次序可能不同,同时还要除去括号。所以在转换时需要从左到右扫描算术表达式,将遇到的操作数直接存放到后缀表达式中,将遇到的每一个运算符或者左括号都暂时保存到运算符栈,而且先执行的运算符先出栈。
- 伪代码
while (从exp读取字符ch, ch = '�')
{
ch为数字:将后续的所有数字均依次存放到postexp中,并以字符'#'标识数字串结束;
ch为左括号'(':将此括号进栈到Optr中;
ch为右括号')':将Optr中出栈时遇到的第一个左括号'('以前的运算符依次出栈并存放到postexp中,然后将左括号'('出栈;
ch为其他运算符:
if (栈空或者栈顶运算符为'(') 直接将ch进栈;
else if (ch的优先级高于栈顶运算符的优先级)
直接将ch进栈;
else
依次出栈并存入到postexp中,直到ch的优先级高于栈顶运算符,然后将ch进栈;
}
若exp扫描完毕,则将Optr中的所有运算符依次出栈并存放到postexp中。
while (从exp读取字符ch, ch != '�')
{
ch为数字:将后续的所有数字均依次存放到postexp中,并以字符'#'标识数字串结束;
ch为左括号'(':将此括号进栈到Optr中;
ch为右括号')':将Optr中出栈时遇到的第一个左括号'('以前的运算符依次出栈并存放到postexp中,然后将左括号'('出栈;
ch为'+'或'-':出栈运算符并存放到postexp中,直到栈空或者栈顶为'(',然后将ch进栈;
ch为'*'或'/':出栈运算符并存放到postexp中,知道栈空或者栈顶运算符为'('、'+'或'-',然后将ch出栈;
}
若exp扫描完毕,则将Optr中的所有运算符依次出栈并存放到postexp中。
- 代码
void trans(char* exp, char postexp[])
{
char e;
SqStack* Optr;
InitStack(Optr);
int i = 0;//i为postexp的下标
while (*exp != '�')//exp表达式未扫描完时循环
{
switch (*exp)
{
case'('://判定为左括号
Push(Optr, '(');//左括号进栈
exp++;//继续扫描其他字符
break;
case')'://判定为右括号
Pop(Optr, e);//出栈元素e
while (e != '(')//不为'('时循环
{
postexp[i++] = e;//将e存放到postexp中
Pop(Optr, e);
}
exp++;
break;
case'+':
case'-':
while (!IsEmpty(*Optr))
{ GetTop(Optr, e);
if (e != '(')
{ postexp[i++] = e;
Pop(Optr, e);
}
else break;
}
Push(Optr, *exp);
exp++;
break;
case'*':
case'/':
while (!IsEmpty(*Optr))
{ GetTop(Optr, e);
if (e == '*' || e == '/')
{ postexp[i++] = e;
Pop(Optr, e);
}
else break;
}
Push(Optr, *exp);
exp++;
break;
default://处理数字字符
while (*exp >= '0' && *exp <= '9')
{ postexp[i++] = *exp;
exp++;
}
postexp[i++] = '#';//用'#'标识一个数字串结束
}
}
while (!IsEmpty(*Optr))//扫描完毕,栈不为空时循环
{ Pop(Optr, e);
postexp[i++] = e;//将e存放到postexp中
}
postexp[i] = '�';//给postexp表达式添加结束标识
DestroyStack(*Optr);
}
1.3队列
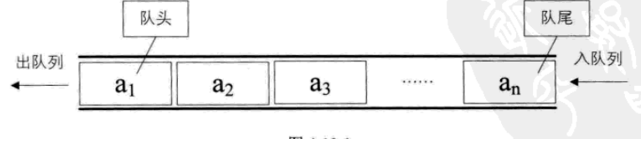
- 队列:队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
- 插入新元素,新元素进队后为新的队尾元素,元素出队后,其后继的元素称为队头元素。
- 队的特点为先进先出
1.3.1顺序队列
- 顺序队结构体定义:
typedef struct
{
ElemType data[MaxSize];
int front,rear;//队首,队尾指针
}Queue;
- 初始化队列:
void InitQueue(Queue &q)
{
q=new Queue;//动态申请内存
q->front=q->rear=-1;
}
- 是否为空队:
bool IsEmpty(Queue &q)
{
if(q.rear==q.front)//队空
return true;
else//队不空
return false;
}
- 进队:
bool enQueue(SqQueue &q,ElemType e)
{
if(q->rear+1==MaxSize)//判断是否栈满
return flase;
q->rear=q->rear+1;//移动指针
q->data[q->rear]=e;
return ture;
}
- 出队:
bool deQueue(SqQueue &q,Elemtype &e)
{
if(q->front==q->rear)//判断队是否为空
return flase;
e=q->data[q->front];
q->front=q->front+1;//移动指针
return ture;
}
- 取队头元素:
bool GetFront(Queue q,Elemtype &e)
{
if(IsEmpty(q))//取队头是要判断是否为空队;
return false;
else
e = q.data[q.front + 1];
return true;
}
- 销毁队列:
void DestroyQueue(Queue &q)
{
delete q;
}
1.3.2环形队列
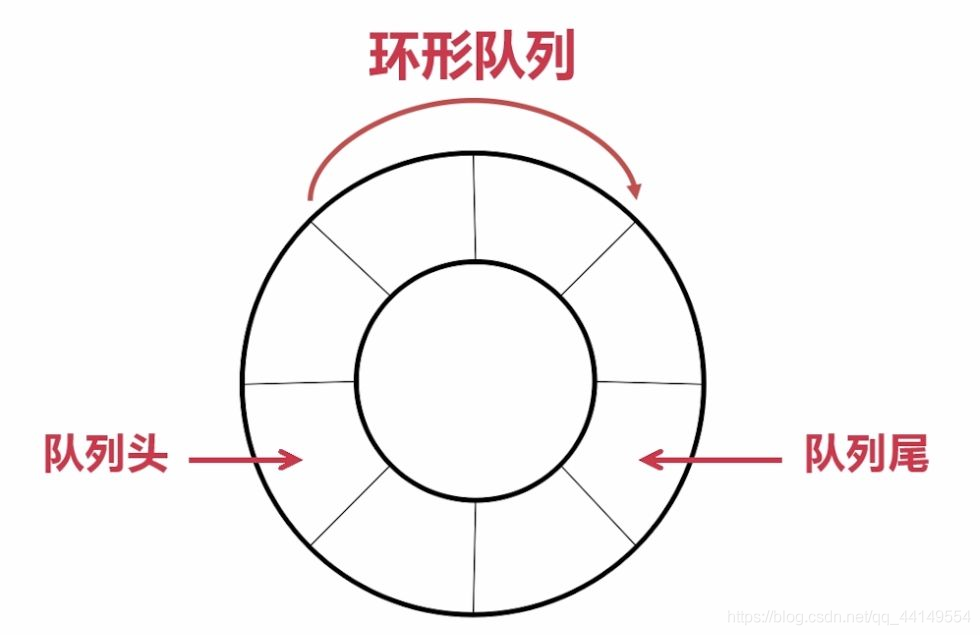
- 初始化队列:
void InitQueue(SqQueue &q)
{
q=new Queue;//动态申请内存
q->front=q->rear=0;
}
- 进环形队列:
bool enQueue(SqQueue &q,Elemtype e)
{
if((q->rear+1)%MaxSize==q->front)//判断是否队满
return false;
q->rear=(q->rear+1)%MaxSize;//移动rear
q->data[q->rear]=e;
return true;
}
- 出环形队列:
bool deQueue(SqQueue &q,Elemtype e)
{
if(q->front==q->rear)//判断是否队空
return false
e=q->data[q->front];
q->front=(q->front+1)%MaxSize;//移动front
return true;
}
出队需要判断是否对空,判断q->front==q->rea,后移动front指针q->front=(q->front+1)%MaxSize
1.3.3链队列
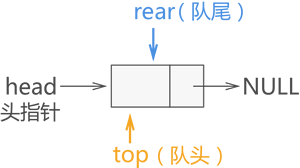
- 初始化链队列:
void InitQueue(LinkQuNode &q)
{
q=new LinkQuNode;
q->front=q->rear=NULL;
}
- 进队列:
bool enQueue(LinkQuNode &q,ElemType e)
{
p=new QNode;
p->data=e;//新建结点
p->next=NULL;//避免后面无结束
q->rear->next=p;
q->rear=p;//尾指针移动
}
- 出队列:
bool deQueue(LinkQuNode &q,ElemType e)
{
Node t;
if(q->rear==NULL)
return false;
t=q->front;
if(q->front==q->rear)//此时只有一个数据
{
q->front=q->rear=NULL;
}
else
{
q->front=q->front->next;//移动front
}
e=t->data;
delete t;//删除
}
1.3.4 C++容器:queue
#include <queue>
q.push(x);将x插入到队列末端,成为新的队尾元素;
q.pop();弹出队列的第一个元素,注意!!这里不返回被弹出元素;
q.front();返回队头元素;
q.back();返回队尾元素;
q.empty();当队空是,返回true;
q.size();返回队列的元素个数;
1.3.5 队列运用
PTA:7-5 报数游戏

#include <iostream>
#include <queue>
using namespace std;
int main()
{
int m;//人数
int n;//数字
queue <int>person;
cin >> m >> n;
if (n > m)//错误情况
{
printf("error!");
}
else
{
int i;
for (i = 1; i <= m; i++)//入队
{
person.push(i);
}
int flag = 1;
int num;
while (!person.empty())
{
i++;
if (i % n == 0)
{
num = person.front();
if (flag == 1)
{
flag = 0;
cout << num;
}
else
{
cout << ' ' << num;
}
person.pop();//出队
i = 0;//重新计数
}
else
{
num = person.front();
person.push(num);//进队
person.pop();//出队
}
}
}
return 0;
}
2.PTA实验作业
2.1 7-3符号配对
2.1.1 解题思路及伪代码
-
解题思路
首先遍历输入数据遇到左符号就入栈;当遇到右符号时应该考虑是否空栈:如果空栈,直接不匹配,输出缺少左符号;如果不为空栈,判断当前的右符号是否与栈顶的左符号匹配:匹配,出栈栈顶元素;不匹配,输出缺少右符号;当遍历结束后,再次考虑:如果为空栈,表示所有的符号都配对,全配对输出;如果不为空栈,说明不配对,输出缺少右符号。 -
伪代码
while(遍历至最后一行)
{
getline(str)
总str += str;
}
用string[]建好左右的符号表。
while(遍历总str中)
{
if(cursign为左符号) 则执行push;
if (cursign为右符号)
{
if(stack不空)
{
if (左右符号匹配) 则执行pop;
else 则执行输出缺右符号
}
else 则执行输出缺左符号
}
if(stack empty) 则all matched
else 则执行输出缺右符号
}
遍历string[]找相同的string元素。
2.1.2 总结解题所用的知识点
本题需要考虑到左符号剩余,右符号剩余,配对情况,不配对情况,需要多重if来进行约束判断。
2.2 7-6 银行业务队列简单模拟
2.2.1 解题思路及伪代码
- 伪代码
输入人数k
创建队列q,p
for (i = 0; i < k; i++)
{
cin >> n;//输入编号
if (n % 2) 编号为奇数则入奇数的栈;
else 编号为偶数则入偶数的栈 ;
}
for (i = 0; i < k; i++)
{
if (i == 0)//对第一个数据输出处理空格
if ((i + 1) % 3)//对a窗口处理
{
if (!q1.empty()//判断是否处理完毕
未处理完毕打出a窗口的编号;
else 处理完毕直接打出b窗口的所有编号;
}
else//对b窗口处理
{
if (!q2.empty())//判断是否处理完毕
未处理完毕打出b窗口的编号
else 处理完毕直接打出b窗口的所有编号
}
}
return 0;
}
2.2.2 总结解题所用的知识点
学会运用queue容器。
3.阅读代码
3.1 题目及解题代码
剑指 Offer 59 - II. 队列的最大值

3.2 该题的设计思路及伪代码
从队列尾部插入元素时,我们可以提前取出队列中所有比这个元素小的元素,使得队列中只保留对结果有影响的数字。这样的方法等价于要求维持队列单调递减,即要保证每个元素的前面都没有比它小的元素。
伪代码:
多加一个双向队列,保存当前的最大值
双向队列里面保证里面数据递减
当push的数据比deque中的数据大时,则将前面的数据剔除,保持递减状态
当pop的数据就是deque最前面的数据,就把deque前面的数据pop掉
代码:
class MaxQueue {
private:
queue<int> myQueue;
deque<int> myDeque;
public:
MaxQueue() {
}
int max_value() {
return myQueue.empty()?-1:myDeque.front();
}
void push_back(int value) {
while((!myDeque.empty())&&(value>myDeque.back()))
{
myDeque.pop_back();
}
myQueue.push(value);
myDeque.push_back(value);
}
int pop_front() {
if(myQueue.empty()){
return -1;
}
int temp=myQueue.front();
if(temp==myDeque.front())
{
myDeque.pop_front();
}
myQueue.pop();
return temp;
}
};
-
时间复杂度:O(1)(插入,删除,求最大值)删除操作于求最大值操作显然只需要 O(1) 的时间
-
空间复杂度:O(n),需要用队列存储所有插入的元素
3.3 分析该题目解题优势及难点
- 从队列尾部取出元素,因此需要使用双端队列来实现。另外我们也需要一个辅助队列来记录所有被插入的值,以确定 pop_front 函数的返回值。

