1)贴上视频学习笔记,要求真实,不要抄袭,可以手写拍照。
二、概率论和贝叶斯先验
1、本福特定律(05:40)
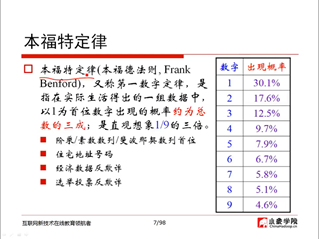
2、概率公式(23:45)
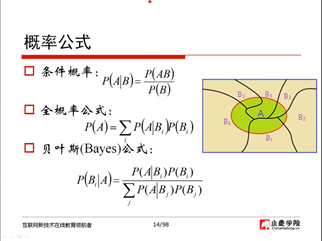
3、贝叶斯公式的应用(28:14)

4、贝叶斯公式(28:38)

5、两点分布(33:02)

6、二项分布(34:38)

7、泊松分布(45:08)

8、均匀分布(48:09)

9、指数分布(48:52)

10、正态分布(53:50)
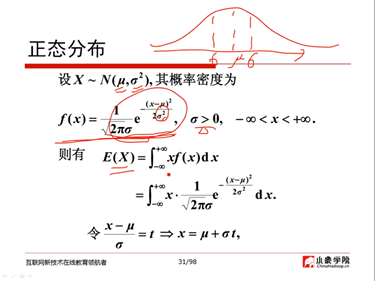
11、Beta分布(61:48)

12、指数族(82:35)

13、事件的独立性(95:08)

14、期望(97:15)

15、方差(103:53)

16、切比雪夫不等式(137:38)

17、大数定律(138:40)

18、中心极限定理(143:51)

三、矩阵和线性代数
1、SVD的提法(04:01)

2、方阵的行列式(16:57)

3、代数余子式(17:58)

4、伴随矩阵(19:26)

5、方阵的逆(20:03)

6、范德蒙行列式(20:18)

7、矩阵的乘法(25:20)

8、矩阵模型(26:12)
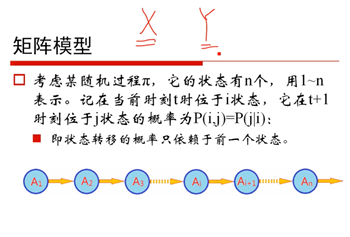
9、概率转移矩阵(31:58)

10、平稳分布(37:37)

11、矩阵和向量的乘法(41:21)

12、矩阵的秩(46:02)

13、向量组等价(52:03)

14、系数矩阵(54:02)

15、正交阵(56:39)

16、特征值和特征向量(59:55)

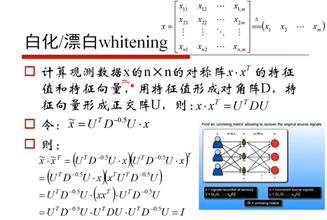
17、白化/漂白(71:39)
18、正定阵(77:35)

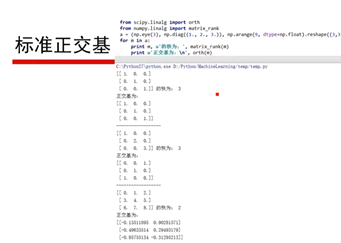
19、标准正交基(82:21)
20、QR分解(84:29)

21、LFM(91:31)

22、向量的导数(94:05)

23、标量对向量的导数(100:46)

24、标量对方阵的导数(101:20)

2)用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”,可以word编辑,可做思维导图,可以手写拍照,要求言简意赅、排版整洁。
答:梯度是一个向量;每个元素为函数对一元变量的偏导数;它既有大小(其大小为最大方向导数),也有方向。在机器学习过程中,经常使用梯度下降方法求解损失函数的最小值。梯度的值为函数在某一点,沿着各向量方向的偏导数。沿着梯度相反的方向,函数减小最快,更容易找到函数的最小值。
梯度下降是优化算法的一种,其思想是让损失函数沿着梯度的方向下降, 以最快的速度取到最小值。
贝叶斯定理:
贝叶斯公式:
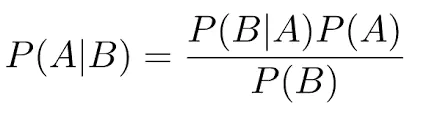
贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。贝叶斯定理,它提供的是一种逆条件概率的方法。