带分数

带分数 

---

问题描述

100 可以表示为带分数的形式：100 = 3 + 69258 / 714。

还可以表示为：100 = 82 + 3546 / 197。

注意特征：带分数中，数字1~9分别出现且只出现一次（不包含0）。

类似这样的带分数，100 有 11 种表示法。

输入格式

从标准输入读入一个正整数N (N<1000*1000)

输出格式

程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。

注意：不要求输出每个表示，只统计有多少表示法！

样例输入1

100

样例输出1

11

样例输入2

105

样例输出2

6

---

Algorithm

一开始，常规思路进行枚举，因为等式形如：

 

那么考虑整除的问题，C最多不超过4位数，A不超过7位数，由等式我们可以算出B。则过程很清晰了：

分别枚举A和C，算出B，判断一下是否满足条件，计数即可。

但是仔细分析了一下时间复杂度，果然没有通过。先放一下代码：

 

/*
* N = A + B/C
* A最多7位，C最多4位,算出B 
*/
#include<iostream>
#include<algorithm>
 
using namespace std;

int c = 0,N = 0;;

// 获取数字长度 
int size(int n)
{
    int c = 0;
    while(n)
    {
        n /= 10;
        c++;
    }
    return c;
}

bool sure(int A, int B, int C)
{
    // 排除有0项 
    if((size(A) + size(B) + size(C)) != 9)
        return false;
    if(A == C)
        return false;
    if(B <= 0)
        return false;
    int s[10] = {0};
    // int a=A,b=B,c=C;
    while(A!=0 || B!=0 || C!=0)
    {
        s[A%10]++;s[B%10]++;s[C%10]++;
        A /= 10;B /= 10;C /= 10;
    }
    for(int i=1;i<=9;i++){
        if(s[i] != 1)
            return false;
    }
    // cout<<a<<":"<<b<<":"<<c<<endl;
    return true;
}

int solve(int n)
{
    // 设置循环节加速，但效果甚小
    int len[7] = {0, 9876, 987, 987, 98, 98, 9};
    int A = 1, C = 2, B = 0;
    for(A=1;A<=9876543;A++){ // 需要排除有0的项 
        // 在这里的几个ABC也可以排除0项，但效果也甚微
        for(C=2;C<=len[size(A)];C++){
            B = C*(N - A);
            if(sure(A, B, C))
                c++;
        }
    }
    return c;
}
/*
* 加速了还是发现时间复杂度太高，约O(9876543 * 5000)
* 改用全排列试试 约O(7 * 9!)
* 速度提升大约 70*30 倍
*/
int main()
{
    while(cin>>N)
    {
        cout<<solve(N)<<endl;
        c = 0;
    }
    return 0;
}

但是思路是没有问题的，接下来想到了以前做过的一道题目：桥本分数式

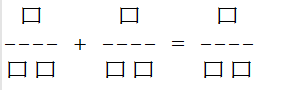
基本与本题一致，所以改用全排列的做法。枚举9个数的全排列确实要比循环每一个A、C快得多。

全排列可以用C++自带的 #include<algorithm> 头文件的 next_permutation 函数。也可以深度优先遍历。

用一个数组保存1 --  9之后，我们只需要尝试每一个组合的有限个分组即可，满足等式计数+1.

尽管还是有点吃力，但是勉强过了。

---

AC

/*
* N = A + B/C
* A 最长不超过7位数, 这样我们确定一个 A 
* 然后我们可以知道 C 的最后一位为 a[8]
* 通过计算我们可以确定 B 的 最后一位 b_end = (N - A)*a[8]%10
* 如此，我们就知道了 C 为多少
* 最后，判断一下是否满足等式 
*/
#include<iostream>
#include<algorithm>
 
using namespace std;

int c = 0,N = 0;;
int a[9] = {1, 2, 3, 4, 5, 6, 7, 8, 9};

// 这里复习一下整数快速幂，就不调用数学库了
// O(log2N)
int pow(int x, int n)
{
    int s = 1;
    while(n)
    {
        if(n&1) s *= x;
        x *= x;
        n >>= 1;
    }
    return s;
}

// A、B、C, b开始, e-1结束的一段数组 
int PI(int b, int e)
{
    int s = 0, k = e-b-1;
    while(b!=e)
    {
        s += a[b]*pow(10, k);k--;b++;
    }
    return s;
}

// 获取 B 最后一位的 local 
int getB_end(int x)
{
    int loc = 0;
    for(int i=0;i<9;i++)
        if(a[i] == x)
            return i;
}

void solve(int *a, int N)
{
    int A, B, C;A = B = C = 0;
    // cout<<N<<endl;
    for(int i=1;i<=7;i++){
        A = PI(0, i);
        int B_end = ((N - A)*a[8])%10;
        int loc = getB_end(B_end);
        if(loc < i || loc >= 8)
            continue;
        // Ai! 这里注意一下是 loc + 1 
        B = PI(i, loc+1);
        C = PI(loc+1, 9);    
        // cout<<A<<":"<<B<<":"<<C<<endl;
        // cout<<A<<":"<<B<<":"<<C<<endl;    
        if(A*C + B == N*C){
            // cout<<A<<":"<<B<<":"<<C<<endl;
            c++;
        }    
    }
}

int main()
{
    while(cin>>N)
    {
        while(next_permutation(a, a+9))
        {   // 时间复杂度可以看成 O(9!) 
            solve(a, N);
            // break;
        }
        cout<<c<<endl;c = 0;
    }
    return 0;
}

---

2019-01-15

19:09:38