包子凑数

包子凑数

---

问题描述

　　小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼，其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼，可以认为是无限笼。


　　每当有顾客想买X个包子，卖包子的大叔就会迅速选出若干笼包子来，使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼，分别能放3、4和5个包子。当顾客想买11个包子时，大叔就会选2笼3个的再加1笼5个的（也可能选出1笼3个的再加2笼4个的）。


　　当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼，分别能放4、5和6个包子。而顾客想买7个包子时，大叔就凑不出来了。


　　小明想知道一共有多少种数目是包子大叔凑不出来的。

输入格式

　　第一行包含一个整数N。(1 <= N <= 100)
　　以下N行每行包含一个整数Ai。(1 <= Ai <= 100)

输出格式

　　一个整数代表答案。如果凑不出的数目有无限多个，输出INF。

样例输入

2
4
5

样例输出

6

样例输入

2
4
6

样例输出

INF

样例说明

　　对于样例1，凑不出的数目包括：1, 2, 3, 6, 7, 11。
　　对于样例2，所有奇数都凑不出来，所以有无限多个。

数据规模和约定

　　峰值内存消耗（含虚拟机） < 256M
　　CPU消耗 < 1000ms




　　请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。


　　注意：
　　main函数需要返回0;
　　只使用ANSI C/ANSI C++ 标准;
　　不要调用依赖于编译环境或操作系统的特殊函数。
　　所有依赖的函数必须明确地在源文件中 #include <xxx>
　　不能通过工程设置而省略常用头文件。


　　提交程序时，注意选择所期望的语言类型和编译器类型。

---

Algorithm

我们先设：

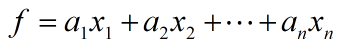
则由不定方程的定理知方程有解的充要条件是：

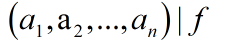
若：

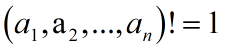
则有无穷个解，直接输出INF。否则，就转化为一个完全背包问题：

有n个物品，它们的价值看做0，每个物品有无限多个。注意到我们的背包容量最大可以取到 100*100，只需要稍微大一点点即可。

看到这里回忆一下完全背包的状态转移方程。

细节问题就看代码吧，debug时间是最长的...

AC

---

 

/*
* 设 f = a1x1 + a2x2 + ··· + anxn; 
* 由不定方程的定理知： 
* (a1, a2,...,an) != 1 则有无穷多个解
* 否则，就是一个完全背包问题(只不过这个背包刚好装满而已）
* (或则说解一个不定方程.......) 
* 回忆一下状态转移方程
*/
#include<iostream>

using namespace std;

const int MAX = 101;
int n, a[MAX] = {0};
const int V = 101*100;
bool f[V] = {0};

int gcd(int a, int b){return (a%b == 0)?b:(gcd(b, a%b));} 

int __cin__(int *a)
{
    cin>>a[0];
    int t = a[0];
    for(int i=1;i<n;i++){
        cin>>a[i];
        t = gcd(a[i], t);
    }
    return t; 
}

int main()
{
    while(cin>>n)
    {
        int s = __cin__(a);
        /* 
        * 这里考虑一下特殊数据：
        * 当两笼包子容量一样，如 3 3 时
        * 仍然有无数种凑不出来，但是gcd(3, 3) = 3 
        * 但是最后发现弄错了，需仔细思考 
        */ 
        if(s != 1) cout<<"INF"<<endl;
        /*next*/
        else{    // 动态规划 ,装满则说明这个容量可行 
            f[0] = true;
            for(int i=0;i<n;i++)
                for(int j=0;j+a[i]<=V;j++){
                    if(f[j]) f[j+a[i]] = true; 
                }
        int c = 0;
        for(int i=0;i<=V;i++)
            if(!f[i]) c++;
        cout<<c<<endl;
        }
        
    }
    
    return 0;
 } 

---

2019-01-15

19:32:59