本讲内容：
1.linear regression(线性回归）
2.gradient descent（梯度下降）
3.normal equations（正规方程组）
首先引入一些符号：
(1) 
训练样本的数量
(2) 
输入变量/ 输入特征
(3) 
输出变量/ 目标变量
(4) 
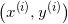第i个训练样本
(5) 
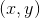训练集
(6) 
特征的数量
监督学习流程图
首先找到一个训练集合（m个样本），提供给学习算法，得到一个输出函数h，称之为假设（hypothesis），这个假设可以对新数据x（不在训练集中的）得到一个新的估计y，即假设h的作用是将输入x映射到输出y。
1.线性回归
问题引入
房屋价格预测
通常情况下许多回归问题都需要多个输入特征，例如房屋价格问题，除了房屋面积之外，还可能有卧室数目这一特征。
在这个例子中，x1表示房屋的size，x2表示卧室数目
因此假设可以这样写：
给定房子的特征x，得到预测的开销 
为了便捷显示，定义
所以
可以表示为 
其中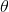
或者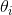 
称之为学习算法的参数， 利用训练集合选择或学习得到合适的参数值，是学习算法的任务。
那么，如何选择参数，使得我们的假设可以对所有房屋做出准确的预测？
引入成本函数的概念，我们希望我们选择的 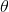可以使得假设对于每一个输入特征得到的预测值
与样本真实标签之间的平方差尽可能小.
定义 
那么该学习算法的任务即为 
2.梯度下降法
在选定线性回归模型后，只需要确定参数 θ，就可以将模型用来预测。然而 θ 需要在 J(θ) 最小的情况下才能确定。因此问题归结为求极小值问题，使用梯度下降法。
梯度下降算法的步骤：
(1) start with some 
(say 
= 
)
(2) keep chaning to reduce 
改变的 值由 对 的偏导数决定。因为求得是的极小值，因此向着偏导数的反方向更新。
梯度下降公式：
注意符号 “:=” 意味着将符号右侧的值赋给左侧
“=” 意味着 真值断言（左侧的值等于右侧）
因此
repeat until convergence
对于有m个训练样本的梯度下降法，更一般的更新公式为
该方法称为批梯度下降 (batch gradient descent)。
如果m是一个百万级的数，即训练集合非常大的时候，使用批梯度下降，收敛速度将是非常慢的。
迭代更新的方式有两种：批梯度下降和随机梯度下降。
随机梯度下降 (stochastic gradient descent) 或者 增量梯度下降 定义如下:
repeat until convergence
{
for j = 1 to m
{
for all i
do 
}
}
当训练集合非常大的时候，随机梯度下降要比批梯度下降算法快得多。
定义新的矩阵求导符号：
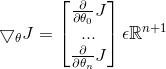
则 
(
是n+1维的数组)
3.正规方程组
对于最小二乘回归问题，不需要采用梯度下降更新参数，而可以直接推出参数
的解析表达式。
引入一些事实：
(1) 如果 
， 
(2) 
(3) 
(4) 
函数f以矩阵A为输入，以实数为输出，所以
(5) 
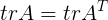如果
, 
(6) 
利用上述事实快速求出使
取最小值的
所以
显然
因此求解
，即可解出
的解析表达式：
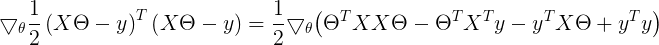
因为
是一个实数，而实数的迹等于实数本身。
因此上式继续推导
利用之前的结论(6)
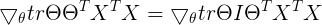
利用之前的结论(4)
解得
该方法的缺陷：X列满秩，而且当特征的数量特别大的时候，求矩阵的逆会非常的慢。
第二讲完。