本讲内容
1. Newton's method（牛顿法）
2. Exponential Family（指数簇）
3. Generalized Linear Models(GLMs)（广义线性模型）
1.牛顿法
假如有函数
, 寻找
使得
牛顿法的步骤如下：
(1) initialize 
as some value. 上图中用 
初始化
的值
(2) 在这一点上对f求值得到
，之后计算这一点的导数值
(3) 作该点的切线，得到与横轴的交点的值
，此为牛顿法的一次迭代。
更新公式为
我们可以使用牛顿法取代梯度上升法作极大似然估计
对对数似然函数
， want 
s.t. 
对于一次迭代，
通常来说，牛顿法对函数f有一定的要求（具体没说），牛顿法对logistic函数效果很好。
的初始值并不会对牛顿法收敛的结果产生影响。
牛顿法的收敛属于二次收敛（每一次迭代都会使误差的数量级乘方），正常情况下速度会比二次收敛慢，但是依然比梯度下降法快。
牛顿法的一般化：
H is the Hessian matrix（黑塞矩阵） 
牛顿法的缺点是，当特征数量过大的时候，求黑塞矩阵的逆会耗费相当长的时间。
2.指数簇
指数簇的一般形式
-自然参数(natural parameter)
- 充分统计量(sufficient statistic) 通常情况下（伯努利分布或者高斯分布）: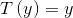 
固定a,b,T， 改变的值， 会得到一组不同的概率分布。
伯努利分布和高斯分布都是指数分布簇的特例
对于伯努利分布
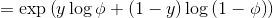
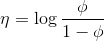
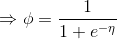
对于高斯分布
考虑到方差对最终结果没有影响， 在这里设置
指数分布族还包括很多其他的分布：
多项式分布（multinomial）
泊松分布（poisson）：用于计数的建模
伽马分布（gamma），指数分布（exponential）:用于对连续非负的随机变量进行建模
β分布，Dirichlet分布：对小数建模
3.广义线性模型(GLMS)
为了导出广义线性模型，首先制定三个假设：
(1) 
(2) Given 
, goal is to output 
want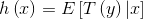 
(3) 
即自然参数与特征向量之间是线性相关的
对于伯努利分布
在上节的指数簇中推导出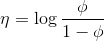
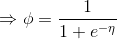
而根据假设(3) 
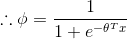
我们的目标是输出 
由上节知
而
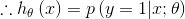
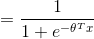
该函数即为logistic 函数
对于高斯分布
在最小二乘估计中，我们假设响应变量是连续的，且服从高斯分布 
我们的目标是输出
由上节知
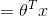
顺带一提
正则响应函数（canonical response function）：
正则链接函数（canonical link function）:
4.Softmax回归（多类分类问题）
多项式分布 
这k个参数是冗余的，所以 我们定义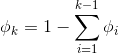 
在后面的过程中，我们将不使用 
这个参数
多项式分布属于指数分布簇，但是 
在这里按照如下定义
... 
都是k-1维的向量
引入指示函数
, 
用 
表示向量
的第
个元素，则 
where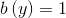 
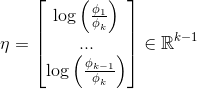
反过来，
为了减少参数冗余，定义
由GLMS的假设3: 
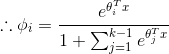
所以我们可以得到需要的假设
这种方法是logistic回归的推广，应用于多分类问题。
优化目标依然是极大似然估计
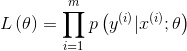
其中
使用梯度上升法或者牛顿法解得最优参数
第四讲完。