岭回归
岭回归是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。
使用sklearn.linear_model.Ridge进行岭回归
一个简单的例子
from sklearn.linear_model import Ridge
clf = Ridge(alpha=.5)
X = [[0,0],[0,0],[1,1]]
y = [0,.1,1]
clf.fit(X,y)
print(clf.coef_)
print(clf.intercept_)
运行结果如下:
使用方法
实例化
Ridge类已经设置了一系列默认的参数,因此clf = Ridge()即可以完成实例化。
但是,了解一下它的参数还是有必要的:
-
alpha:正则化项的系数 -
copy_X:是否对X数组进行复制,默认为True,如果选False的话会覆盖原有X数组 -
fit_intercept:是否需要计算截距 -
max_iter:最大的迭代次数,对于sparse_cg和lsqr而言,默认次数取决于scipy.sparse.linalg,对于sag而言,则默认为1000次。 -
normalize:标准化X的开关,默认为False -
solver:在计算过程中选择的解决器auto:自动选择svd:奇异值分解法,比cholesky更适合计算奇异矩阵cholesky:使用标准的scipy.linalg.solve方法sparse_cg:共轭梯度法,scipy.sparse.linalg.cg,适合大数据的计算lsqr:最小二乘法,scipy.sparse.linalg.lsqrsag:随机平均梯度下降法,在大数据下表现良好。
注:后四个方法都支持稀疏和密集数据,而
sag仅在fit_intercept为True时支持密集数据。 -
tol:精度 -
random_state:sag的伪随机种子
以上就是所有的初始化参数,当然,初始化后还可以通过set_params方法重新进行设定。
回归分析
在实例化Ridge类以后,就可以直接使用Ridge中集成的方法来进行回归了,与绝大多数的sklearn类一样,Ridge使用fit方法执行计算
fit(X,y,sample\_weight=None):X是一个array类型,这是特征矩阵,包含着数据集每一条记录的特征值(N*M),y是结果矩阵,同样是array类型,可以是N*1的形状,也可以是N*K的形状,sample_weight代表着权重,可以是一个实数,也可以给每一条记录分配一个值(array类型)。
得到回归函数后,我们可以通过predict来使用回归函数。
predict(X):X测试数据集,此方法将返回回归后的结果
对于模型的好坏,Ridge当然提供了评价的方法——score
score(X,y,sample_weight=None):X为测试数据,y是测试数据的实际值,类型与fit中的相同,sample是权重
在sklearn中并没有提供直接的查看回归方程的函数,因此查看的时候需要自己转化一下。其实,sklearn就是把相关系数和残差分开保存了,因此,查看的时候要调用coef_和intercept_两个属性。
coef_:相关系数(array类型)intercept_:截距,在fit_intercept=False的时候,将会返回0
可能有用的方法
这些方法在sklearn的基类中就已经集成,但在一般情况下,通常不会用到。
get_params(deep=True):这是获取Ridge实例属性取值的方法,可以忽略set_params(**params):与get_params方法相对,是设置属性值,在岭回归中还是比较重要的,毕竟岭回归的alpha值在一开始可能并不知道,需要在一个范围内进行尝试,因此,利用这个方法来设置alpha值还是比较有用的。
以上就是Ridge的总体介绍,在现实生活中,一般不会想上面的实例中的直接使用定值来计算,下面是一个更实际一点的例子:
# Author: Fabian Pedregosa -- <fabian.pedregosa@inria.fr>
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
###############################################################################
# Compute paths
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
clf = linear_model.Ridge(fit_intercept=False)
coefs = []
for a in alphas:
clf.set_params(alpha=a)
clf.fit(X, y)
coefs.append(clf.coef_)
###############################################################################
# Display results
ax = plt.gca()
ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
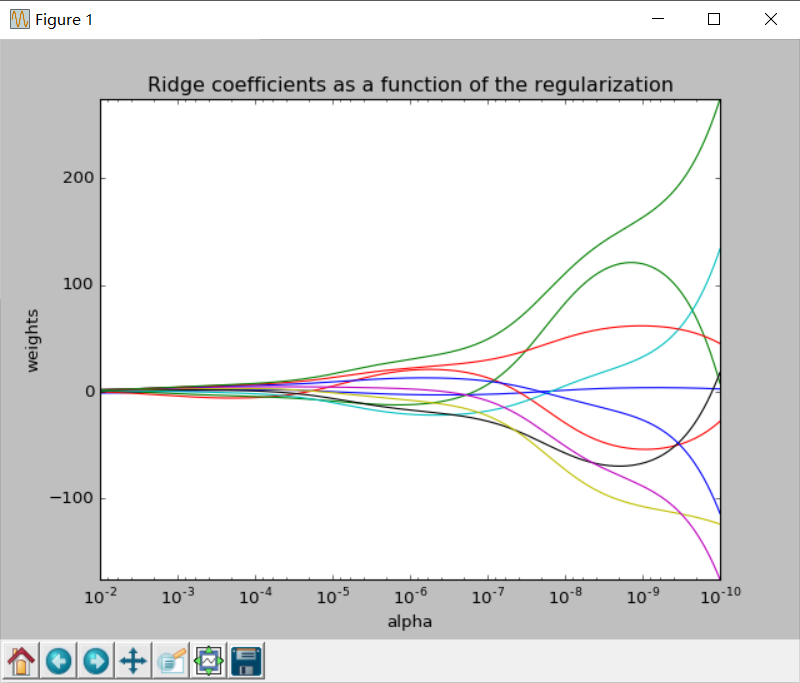
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()
这个例子中,alpha为1e-10~1e-2,以对数值等分,对每一个aplha进行一次计算,最后画出岭迹图。岭迹图的样子如下:
到此,岭回归的内容就结束了,我是sklearn的小小搬运工^_^/