对称二叉树

题目来自：

https://leetcode-cn.com/problems/symmetric-tree/

 方法：递归

如果一个树的左子树与右子树镜像对称，那么这个树是对称的。

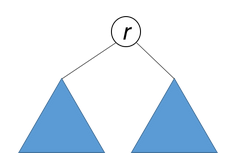
因此，该问题可以转化为：两个树在什么情况下互为镜像？

如果同时满足下面的条件，两个树互为镜像：

1. 它们的两个根结点具有相同的值。
2. 每个树的右子树都与另一个树的左子树镜像对称。

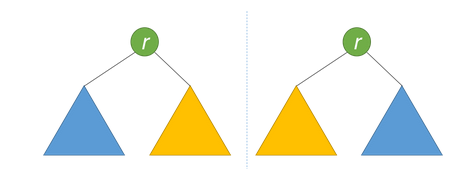
就像人站在镜子前审视自己那样。镜中的反射与现实中的人具有相同的头部，但反射的右臂对应于人的左臂，反之亦然。

上面的解释可以很自然地转换为一个递归函数，如下所示：

public boolean isSymmetric(TreeNode root) {
    return isMirror(root, root);
}

public boolean isMirror(TreeNode t1, TreeNode t2) {
    if (t1 == null && t2 == null) return true;
    if (t1 == null || t2 == null) return false;
    return (t1.val == t2.val)
        && isMirror(t1.right, t2.left)
        && isMirror(t1.left, t2.right);
}

复杂度分析

• 时间复杂度：O(n)。因为我们遍历整个输入树一次，所以总的运行时间为 O(n)，其中 n是树中结点的总数。
• 空间复杂度：递归调用的次数受树的高度限制。在最糟糕的情况下，树是线性的，其高度为 O(n)。因此，在最糟糕的情况下，由栈上的递归调用造成的空间复杂度为 O(n)。

方法二：迭代

除了递归的方法外，我们也可以利用队列进行迭代。队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像。

最初，队列中包含的是 root 以及 root。该算法的工作原理类似于 BFS，但存在一些关键差异。

每次提取两个结点并比较它们的值。然后，将两个结点的左右子结点按相反的顺序插入队列中。

当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

public boolean isSymmetric(TreeNode root) {
    Queue<TreeNode> q = new LinkedList<>();
    q.add(root);
    q.add(root);
    while (!q.isEmpty()) {
        TreeNode t1 = q.poll();
        TreeNode t2 = q.poll();
        if (t1 == null && t2 == null) continue;
        if (t1 == null || t2 == null) return false;
        if (t1.val != t2.val) return false;
        q.add(t1.left);
        q.add(t2.right);
        q.add(t1.right);
        q.add(t2.left);
    }
    return true;
}

复杂度分析

• 时间复杂度：O(n)。因为我们遍历整个输入树一次，所以总的运行时间为 O(n)，其中 n 是树中结点的总数。
• 空间复杂度：搜索队列需要额外的空间。在最糟糕的情况下，我们不得不向队列中插入 O(n) 个结点。因此，空间复杂度为 O(n)。

 

为了得到而努力

2019-04-12

转载请注明来处