斜率优化
1.概念
对于某些转移方程形如(DP[i] = min / max(DP[j] + f(j)))的DP来说,我们可以使用单调队列将其由(O(n^{2}))优化为(O(n))。但对于一些转移方程形如(DP[i] = min / max(DP[j] + f(i , j)))的DP来说,因为转移中有与(i)有关的表达式,于是就不能贸然地使用单调队列了。这个时候我们需要将斜率优化请上台面。
我们以转移方程形如(DP[i] = min(DP[j] + f(i, j)))的DP为例。
尝试将DP方程化为(DP[i] = {color{red}{(……)}} + {color{green}{(……)}} +{color{orange}{(……)}})的形式。红色的部分为仅与(j)有关的表达式,绿色的部分则与(i)和(j)均有关,橙色的部分只与(i)或常数有关。设红色部分为(y),绿色的部分中与(i)有关的部分为(k),与(j)有关的部分为(x),橙色的部分向左移项与(DP[i])合为(B),这样我们就将其化成了(B = y - kx)的形式,整个问题就转化成了求(B)最小。因为在(B)中与(i)有关的部分在单次转移时相当于一个常数,所以求(B)最小就相当于求(DP[i])最小。
对于任意(j),可以表示为坐标轴上一点((x, y)),转移时则可利用坐标计算(y - kx),求得(B)的最小值(当然算的时候别忘了计算(B)中的常数)。保证斜率(k >0),且随(i)单增,才可以进行下面的转移。
如何确定转移最优一点呢?这样:
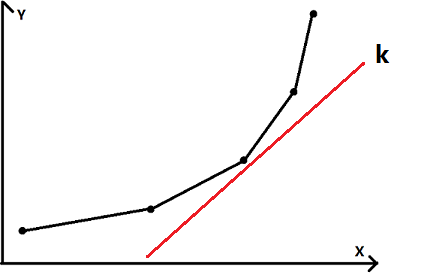
将斜率为(k)的直线上移,可发现第一个触及直线的点会使其截距最小。而又因为斜率单增,所以说此点前的所有点已经对转移没有贡献,直接弹出即可。
如果尾部在插入新的(j)时出现了不下凸的情况怎么办?这样:
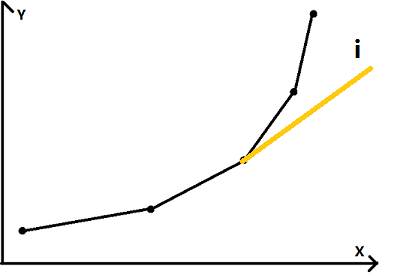
在(i)点之上的两个点在(i)点插入后,将不会有对转移做出贡献的机会,因为由(i)点转移至当前点时所得到的截距将恒优于(i)点之上的两个点。所以此两点一并弹出即可。
或使用数学方法证明:记(slope(i, j) = dfrac{Y(i) - Y(j)}{X(i) - X(j)}),当前点为(l)。若(slope(i, j) < k (i < j)),则说明由(j)转移到(l)较由(i)转移到(l)更优。假设(slope(i, j) > slope(j, l)),若(slope(j, l) < k),则(l)较(j)更优;若(slope(j, l)>k),则(slope(i, j)>k),说明(i)较(j)更优。
这样的话不论怎样,出现上凸的(j)点都不会是更优的转移点,所以说直接将(j)点删除,再(i,l)相连即可。
存点的结构考虑单调队列,因其可以按条件进行双向删除,单向插入,符合需求。
维护队首时,比较(slope(head, head + 1))是否小于(k)。小于(k)说明此点在所求点之下,弹出。第一个(slope(…) geqslant k)的点即为所求转移点。(PS:如果弹到队尾都没有符合要求的点,则至少要留下一个点转移。)
维护队尾时考虑上述证明,弹出(slope(tail, i) < slope(tail - 1, tail))的(tail)。这个就不用留点了,因为到最后还会插入一个(i)。
成型后的有效点集大概这样,是个上凸包。
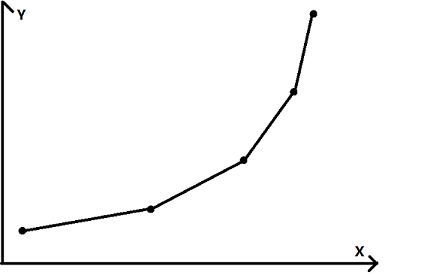
大概就这样。
那么如果(k)随(i)单减,转移方程求的是最小值呢?维护一个上凸包即可(维护单调队列时把小于号都反过来)。
上面所说的均是(x)单调且(k)单调的情况,那如果它们不单调呢?据说(x)不单调可以开平衡树或cdq分治,(k)不单调二分查找。然而我并不会:P。
没了。
2.例题
直接看博客即可。
1.[HNOI 2008]玩具装箱
2.[USACO08MAR] 土地购买 Land Acquisition
有不正确之处请不吝赐教。评论区在下方,若评论框过小右下角拖动即可。谢谢。