「算法笔记」组合数学入门

下面的不用看了，直接看 这里 吧 QAQ（内容更多，更详细，只不过没写二项式定理）

排列组合

一些定义

加法原理：若完成一件事的方法有 n 类，其中第 i 类方法包括 a_i 种不同的方法，且这些方法互不重合，则完成这件事共有 a₁+a₂+...+a_n 种不同的方法。

乘法原理：若完成一件事需要 n 个步骤，其中第 i 个步骤有 a_i 种不同的完成方法，且这些步骤互不干扰，则完成这件事共有 a₁×a₂×...×a_n 种不同的方法。

排列：把 n 个不同元素重新排列，方案数：n!

从 n 个不同元素中一次取出 m 个元素排成一列，产生的不同排列的数量为：

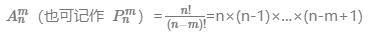
组合：从 n 个不同元素中选出 m 个组成一个集合（不考虑顺序），产生的不同集合数量为：

插板法：x₁+x₂+...+x_n=m 的正整数解的个数为 C(n-1,m-1)。

一些性质

C(n,m)=C(n,n-m)，规定C(n,0)=1,C(n,n)=1

证明：对于从n个不同元素中取出m个组成的每个集合，剩余未取的元素也构成一个集合，两个集合一一对应。

C(n,m)=C(n-1,m)+C(n-1,m-1)

证明：从n个不同元素中取出m个组成一个集合有两类方法：取n号元素、不取n号元素。若取n号元素，则应在剩余n-1个元素中选出m-1个，有C(n-1,m-1)种取法。若不取n号元素，则应在剩余n-1个元素中选出m个，有C(n-1,m)种取法。根据加法原理得，C(n,m)=C(n-1,m)+C(n-1,m-1)。

C(n,0)+C(n,1)+C(n,2)+...+C(n,n)=2ⁿ

证明：从n个不同元素中取出若干个元素组成一个集合，有n+1类方法，分别是取出0,1,2,...n个。根据加法原理共有C(n,0)+C(n,1)+C(n,2)+...+C(n,n)种方法。从另一个方面想，n个元素每个元素可以取或不取，总方法数为2ⁿ，二者相等。

组合数的求法

1.用递推法。C(n,m)=C(n-1,m)+C(n-1,m-1)。复杂度O(n²)。

c[0][0]=1;
for(int i=1;i<=n;i++){
    c[i][0]=1;
    for(int j=1;j<=i;j++)
        c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
} 

2.若题目要求C(n,m)%p的值，并且1~n都存在模p的乘法逆元，则可以先计算分子 n! mod p，再计算分母 m! (n-m)! mod p的逆元，乘起来得到 C(n,m)%p。复杂度为O(n)。

若在计算阶乘的过程中，把 0≤k≤n 的每个 k! mod p 及其逆元分别保存在两个数组 fac 和 inv中，则可以在 O(n log n) 的预处理后，以 O(1) 的时间回答 0≤y≤x≤n 的所以组合数 C(x,y)%p=fac[x]×inv[y]×inv[x-y]%p。

//快速幂： 
int mul(int x,int n,int mod){
    int ans=mod!=1;
    for(x%=mod;n;n>>=1,x=x*x%mod)
        if(n&1) ans=ans*x%mod;
    return ans;
}
//对阶乘数及其逆元进行预处理：
void init(){ 
    f[0]=g[0]=1;
    for(int i=1;i<=n;i++)
        f[i]=f[i-1]*i%mod;    //f(i)表示i! 
    g[n]=mul(f[n],mod-2,mod);    //求逆元 
    for(int i=n-1;i;i--)
        g[i]=g[i+1]*(i+1)%mod;     //g(i)表示 1/(i!) 
} 
//之后就可以调用：
int solve(int n,int m){
    return f[n]*g[m]%mod*g[n-m]%mod;
} 

3.若p为质数，可用Lucas定理求解。（Lucas定理和代码在下文会写）

4.若题目要求对 C(n,m) 进行高精度运算，为避免除法，可把分子、分母快速分解质因数，在数组中保存各项质因子的指数。然后把分子、分母各个质因子的指数对应相减（把分母消去），最后把剩余质因子乘起来，时间复杂度为 O(n log n)。

二项式定理

「NOIP2011」计算系数 题目链接

给定一个多项式 (by+ax)^k，请求出多项式展开后 xⁿy^m 项的系数，对10007取模。0≤n,m≤k≤1000，n+m=k，0≤a,b≤10⁶。

根据二项式定理，有：

所以 xⁿy^m 项的系数即为 C(k,n)aⁿb^m，直接计算 aⁿb^m 和组合数即可。

#include<bits/stdc++.h>
#define int long long
const int N=1010,mod=10007;
int a,b,k,n,m,c[N][N],ans;
int mul(int x,int n,int mod){
    int ans=mod!=1;
    for(x%=mod;n;n>>=1,x=x*x%mod)
        if(n&1) ans=ans*x%mod;
    return ans;
}
signed main(){
    scanf("%lld%lld%lld%lld%lld",&a,&b,&k,&n,&m),c[0][0]=1;
    for(int i=1;i<=k;i++){
        c[i][0]=1;
        for(int j=1;j<=i;j++)
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod; 
    }
    ans=mul(a,n,mod)*mul(b,m,mod)*c[k][n]%mod;
    printf("%lld
",ans);
    return 0;
}

Lucas定理

若 p 是质数，则对于任意整数 1≤m≤n，有：

　　

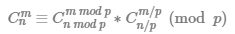
也就是把 n 和 m 表示成 p 进制数，对 p 进制下的每一位分别计算组合数，最后再乘起来。

具体阔以参考这里。

Lucas板子 题目链接

题目大意：求 C(n,m) mod p 的值。

1≤m≤n≤10⁹，m≤10⁴，m<p<10⁹，p 是质数。

直接放个代码叭~ here

#include<bits/stdc++.h>
#define int long long
const int N=1e5+5;
int t,n,m,p;
int mul(int x,int n,int mod){
    int ans=mod!=1;
    for(x%=mod;n;n>>=1,x=x*x%mod)
        if(n&1) ans=ans*x%mod;
    return ans;
}
int C(int n,int m){
    if(m>n) return 0;
    int x=1,y=1;
    for(int i=n-m+1;i<=n;i++) x=x*i%p;
    for(int i=2;i<=m;i++) y=y*i%p;
    return x*mul(y,p-2,p)%p;
} 
int lucas(int n,int m){
    if(!m) return 1;
    return C(n%p,m%p)*lucas(n/p,m/p)%p;
}
signed main(){
    scanf("%lld",&t);
    while(t--){
        scanf("%lld%lld%lld",&n,&m,&p);
        printf("%lld
",lucas(n,m));
    }
    return 0;
}