联合间接排序
联合间接排序支持为待排序列排序,若待排序列值相同,则利用参考序列作为参考继续排序。最终返回排序过后的有序索引序列。
indices = numpy.lexsort((参考序列, 待排序列))
案例:先按价格排序,再按销售量倒序排列。
#排序 import numpy as np names=np.array(['Apple','Mi','Oppo','Vivo','Huawei']) price = [8888,2999,3999,3999,49999] volume = np.array([50,100,90,88,110]) #联合间接排序 sorted_inds = np.lexsort((-volume,price)) print(names[sorted_inds])
复数数组排序
按照实部的升序排列,对于实部相同的元素,参考虚部的升序,直接返回排序后的结果数组。
numpy.sort_complex(复数数组)
插入排序
若有需求需要向有序数组中插入元素,使数组依然有序,numpy提供了searchsorted方法查询并返回可插入位置数组。
indices = numpy.searchsorted(有序序列, 待插序列)
案例:
import numpy as np # 0 1 2 3 4 5 6 a = np.array([1, 2, 4, 5, 6, 8, 9]) b = np.array([7, 3]) c = np.searchsorted(a, b) print(c) d = np.insert(a, c, b) print(d)
scipy提供了常见的插值算法可以通过 一组离散点得到符合这组散点分布规律插值器函数。若我们给插值器函数更多的散点x坐标序列,该函数将会返回相应的y坐标序列。
func = si.interp1d( 离散水平坐标, 离散垂直坐标, kind=插值算法(缺省为线性插值) )
案例:
# scipy.interpolate import scipy.interpolate as si import numpy as np import matplotlib.pyplot as mp # 原始数据 15组数据 min_x = -50 max_x = 50 dis_x = np.linspace(min_x, max_x,15) dis_y = np.sinc(dis_x) mp.scatter(dis_x,dis_y,color='dodgerblue',s=70) #绘制线性插值器函数 通过一系列的散点设计出符合一定规律插值器函数,使用线性插值(kind缺省值) linear = si.interp1d(dis_x,dis_y) x = np.linspace(min_x,max_x,1000) y = linear(x) mp.plot(x,y) # 三次样条插值 (CUbic Spline Interpolation) 获得一条光滑曲线 cubic = si.interp1d(dis_x, dis_y, kind='cubic') cub_x = np.linspace(min_x, max_x, 1000) cub_y = cubic(cub_x) mp.plot(cub_x,cub_y) mp.show()
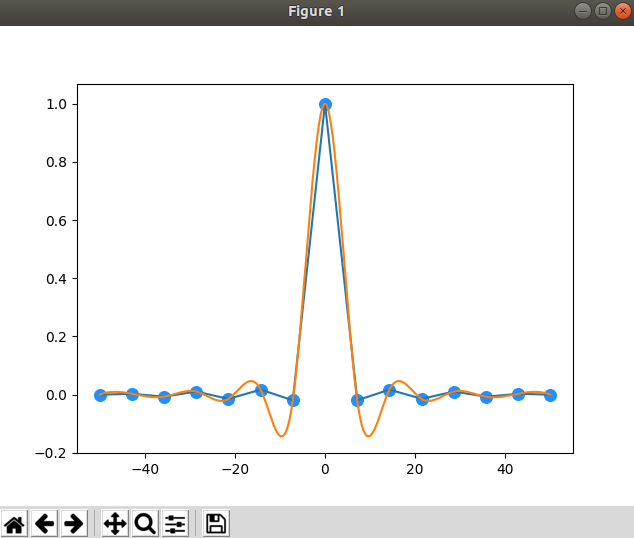
积分
直观地说,对于一个给定的正实值函数,在一个实数区间上的定积分可以理解为坐标平面上由曲线、直线以及轴围成的曲边梯形的面积值(一种确定的实数值)。
利用微元法认识什么是积分。
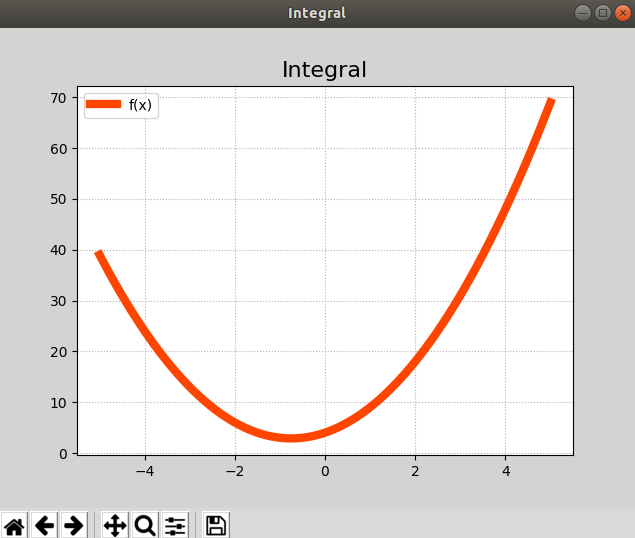
案例:在[-5, 5]区间绘制二次函数y=2x2+3x+4的曲线:
#积分 import numpy as np import matplotlib.pyplot as mp def f(x): return 2*x**2+3*x+4 a,b = -5,5 x=np.linspace(a,b,1000) y=f(x) mp.figure('Integral',facecolor='lightgray') mp.title('Integral',fontsize=16) mp.grid(linestyle=':') mp.plot(x,y,c='orangered',linewidth=6,label='f(x)') #计算f(x)在[-5,5]区间的定积分 n=200 x = np.linspace(a,b,n) y = f(x) area = 0 for i in range(n-1): area+=(y[i]+y[i+1])*(x[1]-x[0])/2 print(area)#206.67508396252612 mp.legend() mp.show()
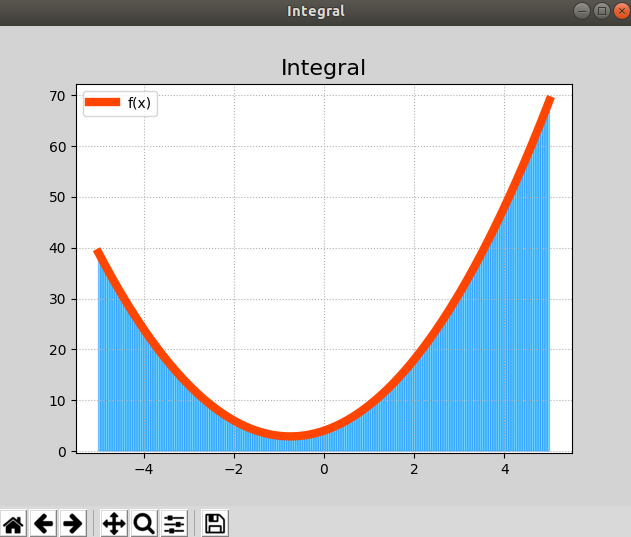
案例:微分法绘制函数在与x轴还有[-5, 5]所组成的闭合区域中的小梯形。
# 积分 import numpy as np import matplotlib.pyplot as mp import matplotlib.patches as mc def f(x): return 2 * x ** 2 + 3 * x + 4 a, b = -5, 5 x = np.linspace(a, b, 1000) y = f(x) mp.figure('Integral', facecolor='lightgray') mp.title('Integral', fontsize=16) mp.grid(linestyle=':') mp.plot(x, y, c='orangered', linewidth=6, label='f(x)') # 计算f(x)在[-5,5]区间的定积分 n = 200 x = np.linspace(a, b, n) y = f(x) area = 0 for i in range(n - 1): area += (y[i] + y[i + 1]) * (x[1] - x[0]) / 2 print(area) # 206.67508396252612 for i in range(n - 1): mp.gca().add_patch(mc.Polygon([ [x[i], 0], [x[i], y[i]], [x[i + 1], y[i + 1]], [x[i + 1], 0]], fc='deepskyblue', ec='dodgerblue', alpha=0.5)) mp.legend() mp.show()
调用scipy.integrate模块的quad方法计算积分:
import scipy.integrate as si # 利用quad求积分 给出函数f,积分下限与积分上限[a, b] 返回(积分值,最大误差) area = si.quad(f, a, b)[0] print(area)
import numpy as np import scipy.integrate as si def f(x): return 2 * x ** 2 + 3 * x + 4 a, b = -5, 5 x = np.linspace(a, b, 1000) y = f(x) #基于scipy求积分 r = si.quad(f, -5, 5) print(r)#(206.66666666666669, 2.294460917558657e-12)
图像
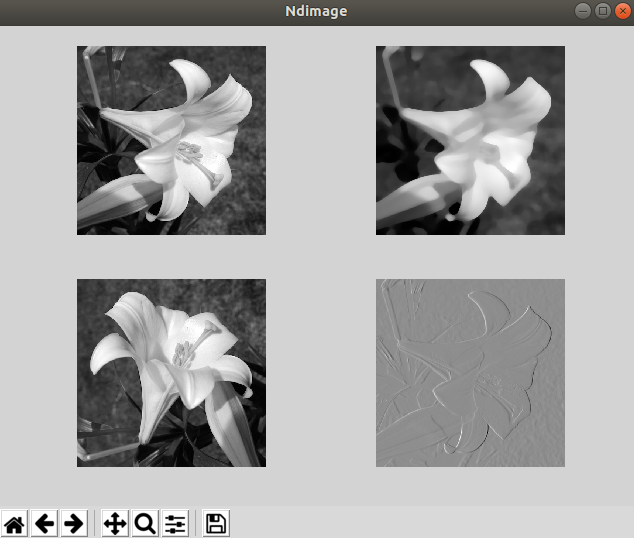
scipy.ndimage中提供了一些简单的图像处理,如高斯模糊、任意角度旋转、边缘识别等功能。
# 图像 import scipy.misc as sm import scipy.ndimage as sn import matplotlib.pyplot as mp # 读取文件 img = sm.imread('lily.jpg', True) print(img.shape)#(512, 512) mp.figure('Ndimage', facecolor='lightgray') mp.subplot(221) mp.axis('off') # 关闭坐标轴 mp.imshow(img, cmap='gray') # 高斯模糊 img2 = sn.median_filter(img, 20) # 数越大越模糊,算法越复杂,越耗时 mp.subplot(222) mp.axis('off') mp.imshow(img2, cmap='gray') # 旋转 img3 = sn.rotate(img, 90) # 逆时针旋转 mp.subplot(223) mp.axis('off') mp.imshow(img3, cmap='gray') # 边缘识别 img4 = sn.prewitt(img) mp.subplot(224) mp.axis('off') mp.imshow(img4, cmap='gray') mp.tight_layout() mp.show()
# 金融相关API import numpy as np # 终值 = np.fv(利率, 期数, 每期支付, 现值) # 将1000元以1%的年利率存入银行5年,每年加存100元, # 到期后本息合计多少钱? fv = np.fv(0.01, 5, -100, -1000) print(round(fv, 2)) # 1561.11 # 现值 = np.pv(利率, 期数, 每期支付, 终值) # 将多少钱以1%的年利率存入银行5年,每年加存100元, # 到期后本息合计2000元? pv = np.pv(0.01, 5, -100, 2000) print(pv) # -1417.588251280984 # 净现值 = np.npv(利率, 现金流) # 将1000元以1%的年利率存入银行5年,每年加存100元, # 相当于一次性存入多少钱? npv = np.npv(0.01, [ -1000, -100, -100, -100, -100, -100]) print(round(npv, 2)) # -1485.34 fv = np.fv(0.01, 5, 0, npv) print(round(fv, 2)) # 1561.11 # 内部收益率 = np.irr(现金流) # 将1000元存入银行5年,以后逐年提现100元、200元、 # 300元、400元、500元,银行利率达到多少,可在最后 # 一次提现后偿清全部本息,即净现值为0元? irr = np.irr([-1000, 100, 200, 300, 400, 500]) print(round(irr, 2)) # 0.12 npv = np.npv(irr, [-1000, 100, 200, 300, 400, 500]) print(npv) # 0.0 # 每期支付 = np.pmt(利率, 期数, 现值) # 以1%的年利率从银行贷款1000元,分5年还清, # 平均每年还多少钱? pmt = np.pmt(0.01, 5, 1000) print(round(pmt, 2)) # -206.04 #多还的钱 print(round(pmt, 2) * 5 + 1000) # -30.200000000000045 # 期数 = np.nper(利率, 每期支付, 现值) # 以1%的年利率从银行贷款1000元,平均每年还pmt元, # 多少年还清? nper = np.nper(0.01, pmt, 1000) print(int(nper)) # 5 # 利率 = np.rate(期数, 每期支付, 现值, 终值) # 从银行贷款1000元,平均每年还pmt元,nper年还清, # 年利率多少? rate = np.rate(nper, pmt, 1000, 0) print(round(rate, 2)) # 0.01