0098. Validate Binary Search Tree (M)

Validate Binary Search Tree (M)

题目

Given a binary tree, determine if it is a valid binary search tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

    2
   / 
  1   3

Input: [2,1,3]
Output: true

Example 2:

   5
   / 
  1   4
     / 
    3   6

Input: [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

---

题意

判断给定树是否为二叉查找树(左/右子树为严格小于/大于关系)。

思路

第一时间想到递归判断左结点小于根结点、右结点大于根结点，但这种做法是错误的，因为可能出现以下这种情况(因为只考虑了左子树根结点小于根节点，实际上要保证左子树所有结点都小于根节点，右子树同理)：

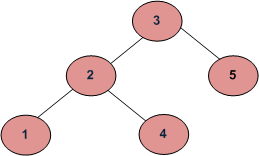
由BST的性质-中序遍历必然得到递增序列，因而可以通过中序遍历给定二叉树，判断序列是否递增对来判断是否是BST。中序遍历方法较多，具体可参考 94. Binary Tree Inorder Traversal。

另一种方法：对第一种方法进行改进，加上最小值、最大值的限定，使得当前结点都必须在(min, max)的范围里。因为测试样例包含了Integer.MAX_VALUE和Integer.MIN_VALUE，所以范围端点要使用long(硬要用int可以再设两个参数minUsed和maxUsed来标记Integer边界值是否已被使用)。

---

代码实现

Java

范围限制

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValid(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    private boolean isValid(TreeNode x, long minValue, long maxValue) {
        if (x == null) {
            return true;
        }

        if (x.val >= maxValue || x.val <= minValue) {
            return false;
        }

        return isValid(x.left, minValue, x.val) && isValid(x.right, x.val, maxValue);
    }
}

中序遍历

class Solution {
    int pre;
    boolean isFirst;

    public boolean isValidBST(TreeNode root) {
        isFirst = true;
        return isValid(root);
    }

    private boolean isValid(TreeNode x) {
        if (x == null) {
            return true;
        }
		
        // 处理左子树
        if (!isValid(x.left)) {
            return false;
        }
      	// 处理当前结点
        if (!isFirst && x.val <= pre) {
            return false;
        }
        if (isFirst) {
            isFirst = false;
        }
        pre = x.val;
        // 处理右子树
        if (!isValid(x.right)) {
            return false;
        }

        return true;
    }
}

JavaScript

/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  return isValid(root, [-Infinity, Infinity])
}

let isValid = function (root, range) {
  if (!root) {
    return true
  }

  if (root.val >= range[1] || root.val <= range[0]) {
    return false
  }

  return isValid(root.left, [range[0], root.val]) && isValid(root.right, [root.val, range[1]])
}