动脑动手:
1、源程序代码:
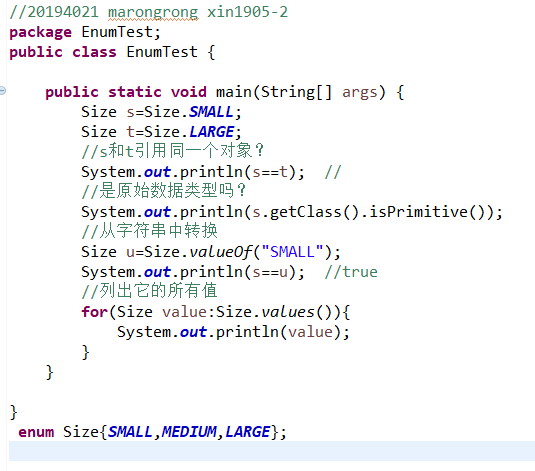
运行结果:
2、
(1)原码:用两个字节(byte,1字节=8位(bite)),16位表示的二进制整数。
如0的原码:0(或1)000 0000 0000 0000
正整数的原码(如1):0000 0000 0000 0001
负整数的原码(如-1):1000 0000 0000 0001
正整数的原码,最高位是0,负整数的原码最高位是1(计算机中最高位0表示正,1表示-),除最高位外其余各位表示这个整数的绝对值即可;
(2)反码:正整数的反码=原码
负整数的最高位不变还是1,其它位取反(0变1,1变0)就得到负整数的反码了,如-1的反码就是:
1111 1111 1111 1110
(3)补码,补码是cpu内部用来计算数据的:
正整数的补码=原码=反码;
将负整数的原码取它的反码,将它的补码加一就得到负整数的补码了。
如数-1:1000 0000 0000 0001
先取反码得:1111 1111 1111 1110
将反码加1就得到补码:1111 1111 1111 1111
注:计算机内部存储的数都是二进制数的补码形式

由上述程序验证可以得知,程序结果为0,而在二进制中00000001+10000001=10000010,换算成二进制结果为-2,显然java中的数值不是由原码储存的
同理,在使用反码表示时,也会出现同样的问题: (00000001) 反+ (11111110)反 = (11111111)反 = ( -0 )
而在补码中这没有这个问题:(00000001)补 + (11111111)补 = (00000000)补 = ( 0 )
所以在java中,数值是由补码表示的。
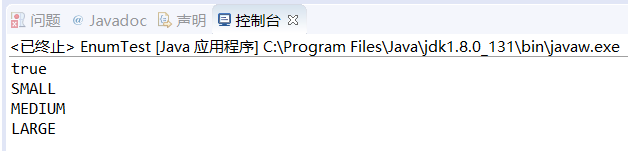
3、源程序代码:

运行结果:

由此可知,每个变量都有一个有效区域,即定义的那片区域,出了这个区域,变量将不再有效(全局变量除外)。
4、源程序代码:
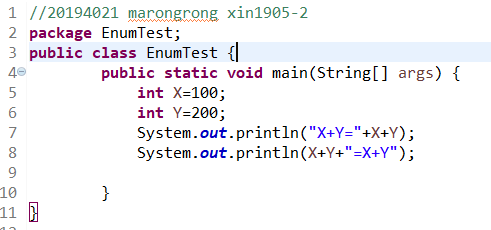
运行结果:

第一句输出中“+”连接字面量,计算结果是将X和Y将两数据连接。
语句二输出中“+”是运算符,计算结果是对X和Y求和。
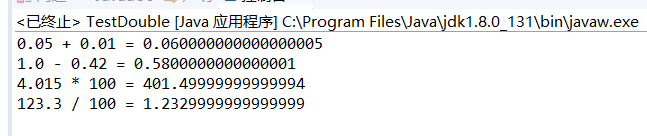
5、为什么double类型的数值进行运算得不到“数学上精确”的结果?
float 和double类型主要是为科学计算和工程计算而设计的,他们执行二进制浮点运算,这两种类型在计算机中的储存分为三部分:符号位、指数为、尾数部分。数据以二进制存储在计算机时,会出现无线循环系列,在数据转化中会出现错误。十进制不能准确的表示1/3,同样二进制不能精确的表示1/10。
动手实验:
1、源程序代码:
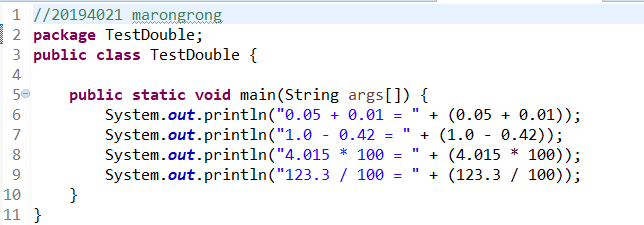
运行结果:
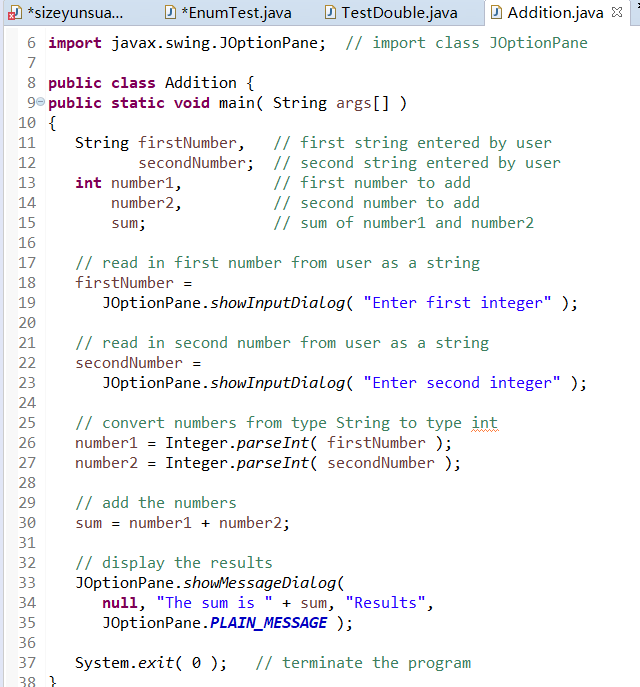
2.Addtion
源程序代码:
运行过程及结果:
3、BigDecimal
源程序代码:
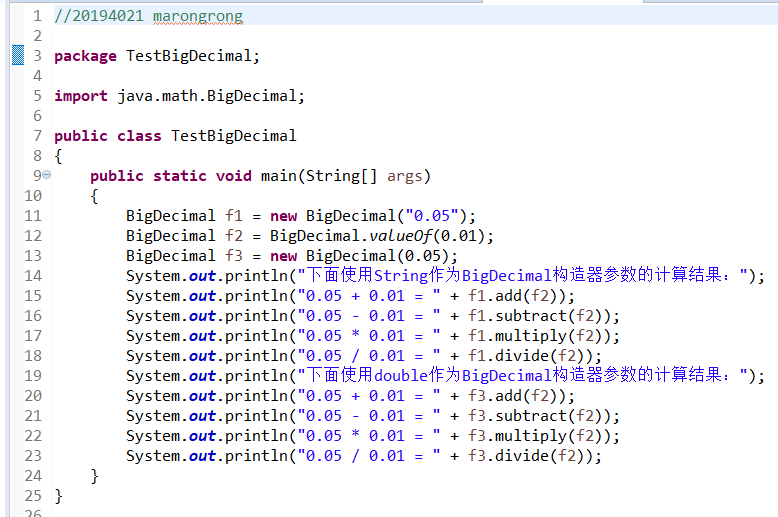
运行结果:
