[题解] luogu P3379 【模板】最近公共祖先（LCA） 树链剖分

刚重温了下LCA，写个题解记录下
Problem

什么是LCA

LCA(Lowest Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先

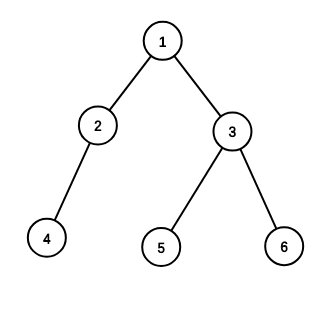
举个例子，如图，4和5的最近公共祖先为1,5和6的最近公共祖先为3

什么是树链刨分

树链剖分，指一种对树进行划分的算法，它先通过轻重边剖分将树分为多条链，保证每个点属于且只属于一条链，然后再通过数据结构（树状数组、BST、SPLAY、线段树等）来维护每一条链，复杂度为(O(logN))

我们令(size[v])为以(v)为根的子树的大小

重边和重链

重边，即(u)与其儿子中(size[v])最大的那个点的连边。
重链，即重边所连成的链

轻边和轻链

轻边，即(u)的重边以外的所有边
轻链，即轻边所连成的链

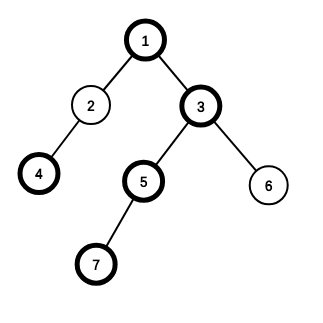
如图，图中加粗的点都在重链上

思路

树刨后，我们可以发现不在重链上的边减少了，
我们不妨设每个节点(v)所在链的顶端为(top[v])，父亲节点为(fa[v])，深度为(dep[v])
两个点(a)，(b)往上找，深度大的点为(a)，(a)往上跳，
如果(a)在重链上，就跳到所在重链的链顶的父亲处，
如果(a)在轻链上，就直接跳到自己父亲上
(都跳到(fa[top[a]]))上

具体实现

• dfs1求出：结点(i)的深度(dep[i])， 以(i)为根的子树大小(siz[i])，结点i的父亲(fa[i])， 并预处理出重链
• dfs2求出：结点(i)所在重链的链顶(top[i])，如果它不为重节点，直接令(top[i] = i;)

int LCA(int a, int b) {
	while (top[a] != top[b]) {
	//链顶相同时，说明这两点在同一条链上了
		if(dep[top[a]] < dep[top[b]]) 
			a = fa[top[a]];
		else b = fa[top[b]];
	}//深度大的向上跳
	if (dep[a] >= dep[b]) return b;
	else return a;
}

时间复杂度应为:(O(2n + mlogn))

CODE

#include <bits/stdc++.h>
#define SIZE 500000
using namespace std;

int n, m, root, x, y, len;
int f[SIZE + 30], Dep[SIZE + 30], siz[SIZE + 30];
int Son[SIZE + 30], Top[SIZE + 30], Fa[SIZE + 30];

struct Edge {
	int s, next;
}e[SIZE * 4 + 30];
inline void AddEdge(int u, int v){
    e[++len] = (Edge){v, f[u]};
    f[u] = len;
}

void dfs1(int s) {//预处理Dep, siz, Fa, Son
	siz[s] = 1;//加上根
	for (int i = f[s]; i; i = e[i].next) {
		int d = e[i].s;
		if (Fa[s] != d) {//保证此边连的不是父亲
			Fa[d] = s;//预处理d的父亲为s
			Dep[d] = Dep[s] + 1;//预处理深度dep
			dfs1(d);//先求出以d为根的子树的大小同时预处理下面的dep,fa,son
			siz[s] += siz[d];//以s为根的子树大小相应加上以d为根的子树大小
			if (siz[Son[s]] < siz[d])
				Son[s] = d;//查找重节点
		}
	}
}
void dfs2(int s) {//预处理Top 
	if (s == Son[Fa[s]])
		Top[s] = Top[Fa[s]];//重节点的top就是重链的链顶
	else Top[s] = s;//轻链的链顶为自己
	for (int i = f[s]; i; i = e[i].next)
		if (e[i].s != Fa[s])//保证这条边连的不是父亲
			dfs2(e[i].s);//继续拓展下面的节点的top
}

int LCA(int a, int b) {
	while (Top[a] != Top[b]) {
        //链顶相同时，说明这两点在同一条链上了
		if(Dep[Top[a]] < Dep[Top[b]]) a = Fa[Top[a]];
		else b = Fa[Top[b]];//深度大的向上跳
	}//搜到在同一条链上时，返回深度大的值
	if (Dep[a] >= Dep[b]) return b;
	else return a;
}

int main() {
	scanf ("%d%d%d", &n, &m, &root);
	for (int i = 1; i < n; ++i) {
		scanf ("%d%d", &x, &y);
		AddEdge(x, y); AddEdge(y, x);
	}//前向星加边
	Dep[root] = 1;
	dfs1(root);
	dfs2(root);
	for (int i = 1; i <= m; ++i) {
		scanf ("%d%d", &x, &y);
		printf("%d
", LCA(x, y));
	}//在线处理，离线可以用tarjan但我不会
	return 0;
}