二叉树之三(AVL)

AVL树

AVL的特征

1. 首先,他是一个搜索二叉树
2. 其次，左右子树的(height)之差绝对值不超过1，也就是(1geq{|H|}geq{0})。

---

AVL的调整

1. 单旋转

2. 双旋转

   旋转完成对于该结构的调整，在左左子树操作的时候，右旋，右右子树左旋，左右先左旋后右旋，右左先右旋后左旋。

---

时间复杂度分析

1. 对于一般的搜索树，我们知道插入的操作就是按照顺序进行操作的，可一旦擦喝的数据是一个有序的队列
   那么操作的时间复杂度将会退化成(O(N))，但是实际上我们总是希望在树结构当中，访问时间复杂度总是在
   一个(O(log_2N))的复杂度。
2. AVL应运而生，时间复杂度保持在(O(log_2N))

---

ALV操作

1. 旋转
   如果在一棵AVL树中插入一个新结点，就有可能造成失衡，此时必须重新调整树的结构，使之恢复平衡。我们称调整平衡过程为平衡旋转(rotation)。
   
   对于失去平衡的二叉树可以归纳为4种类型：

• RR型：单向左旋平衡处理
  
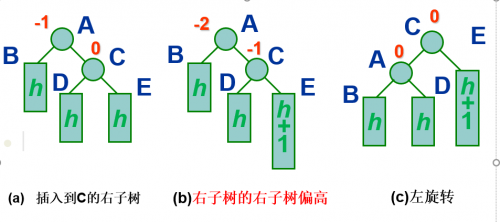
  结点A是插入后失去平衡的最高层结点
  插入后A的右子树的右子树偏高
  则进行左旋转
  
  
• LL型：单向右旋平衡处理
  
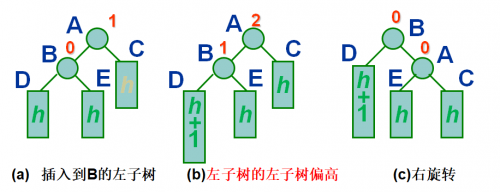
  结点A是插入后失去平衡的最高层结点，
  插入后A的左子树的左子树偏高。
  则进行右旋转。
  
  
• RL型：双向旋转，先右后左
  
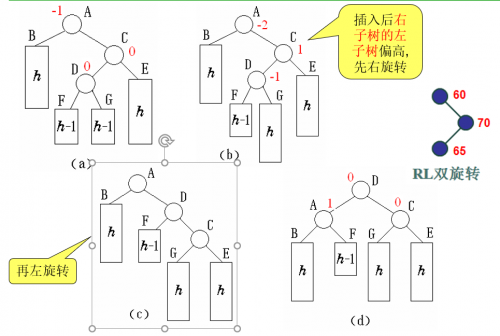
  这一部分可以调用上面实现的单旋转函数。
  
  
• LR型：双向旋转，先左后右
  
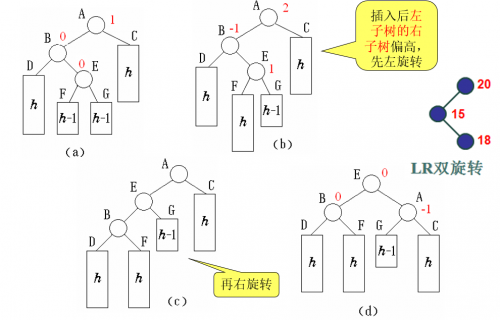
  这一部分可以调用上面实现的单旋转函数。
  
  

2. 插入
   插入操作是在我们的二叉搜索树的基础上面完成的，就是数字小而且左子树空的时候插入左子树，数字大右子树空的时候插入到右边。插入的过程借助递归。另外插入完成之后记得旋转。

3. 实现

#include <iostream>
using namespace std;
#define DataType int
/*
    定义AVL树的结构体，链式
*/
typedef struct AvlNode{
    DataType    data;
    AvlNode    * m_pLeft;
    AvlNode    * m_pRight;
    int height;
}*AvlTree,*Position,AvlNode;

//求两个数的最大值
int Max(int a,int b)
{
    return a>b?a:b;
}
//求树的高度
int Height( AvlTree T)
{
    if(NULL == T)
        return -1;
    else
        return T->height;
}

//单旋转右旋(看图操作) 
AvlTree singleRotateWithRight(AvlTree T)
{
    AvlTree L = T->m_pLeft;
    T->m_pLeft = L->m_pRight;
    L->m_pRight = T;
    T->height = Max( Height(T->m_pLeft),Height(T->m_pRight) ) + 1;
    L->height = Max( Height(L->m_pLeft),Height(L->m_pRight) ) + 1;
    return L;    //此时L成为根节点了（可参考AVL的插入的左左情况的右旋图）
}
//单旋转左旋
AvlTree singleRotateWithLeft(AvlTree T)
{
    AvlTree R = T->m_pRight;
    T->m_pRight = R->m_pLeft;
    R->m_pLeft = T;
    T->height = Max( Height(T->m_pLeft),Height(T->m_pRight) ) + 1;
    R->height = Max( Height(R->m_pLeft),Height(R->m_pRight) ) + 1;
    return R;    //此时R成为根节点了（可参考AVL的插入的左左情况的左旋图）
}
//双旋转，先左后右
AvlTree doubleRotateWithLeft(AvlTree T)        //先左后右
{
    T->m_pLeft = singleRotateWithLeft(T->m_pLeft);
    return singleRotateWithRight(T);
}
//双旋转，先右后左
AvlTree doubleRotateWithRight(AvlTree T)    //先右后左
{
    T->m_pRight = singleRotateWithRight(T->m_pRight);
    return singleRotateWithLeft(T);
}
AvlTree AvlTreeInsert(AvlTree T, DataType x)
{
    if(T == NULL)    //如果树为空
    {
        T = (AvlNode *)malloc(sizeof(struct AvlNode));
        if(T)
        {
            T->data = x;
            T->m_pLeft    = NULL;
            T->m_pRight = NULL;
            T->height = 0;
        }
        else
        {
            cout << "空间不够" << endl;
            exit(0);
        }
    }
    else if( x < T->data)        //如果插入到T结点的左子树上
    {
        T->m_pLeft = AvlTreeInsert(T->m_pLeft,x);    //先插入，后旋转
        if(Height(T->m_pLeft) - Height(T->m_pRight) == 2) //只有可能是这个看图索引
        {
            if(x < T->m_pLeft->data)        //左左情况，只需要右旋转
            {
                T = singleRotateWithRight( T );
            }
            else                            //左右情况，双旋转,先左
            {
                T = doubleRotateWithLeft( T );
            }
        }
    }
    else if( x > T->data )
    {
        T->m_pRight = AvlTreeInsert(T->m_pRight,x);
        if(Height(T->m_pRight) - Height(T->m_pLeft) == 2)
        {
            if(x > T->m_pRight->data)        //右右情况，进行左旋
            {
                T = singleRotateWithLeft( T );
            }
            else                            //左右情况，双旋转,先右
            {
                T = doubleRotateWithRight( T );
            }
        }
    }
    //如果这个数已经存在，那么不进行插入，二叉搜索树性质决定了不能插入相同的数值
    T->height = Max(Height(T->m_pLeft),Height(T->m_pRight)) + 1;
    return T;
}
//递归实现中序遍历
void inOrderVisitUseRecur(const AvlTree pCurrent)//二叉树的遍历三种顺序都会存在
{//下一节的森林一般没有中序的遍历
    if(pCurrent)
    {
        inOrderVisitUseRecur(pCurrent->m_pLeft);
        cout <<"pCurrent->"<<pCurrent->data << " ";
        if(pCurrent->m_pLeft)
            cout << " leftChild->"<<pCurrent->m_pLeft->data<<" ";
        else
            cout << " leftChild->"<<"NULL" <<" ";
        if(pCurrent->m_pRight)
            cout << " rightChild->"<<pCurrent->m_pRight->data<<" ";
        else
            cout << " rightChild->"<< "NULL"<<" ";
        cout << endl;
        inOrderVisitUseRecur(pCurrent->m_pRight);
    }
}
int main()
{
    AvlTree root = NULL;
    root = AvlTreeInsert(root,1);
    root = AvlTreeInsert(root,2);
    root = AvlTreeInsert(root,3);
    root = AvlTreeInsert(root,4);
    root = AvlTreeInsert(root,5);
    root = AvlTreeInsert(root,6);
    root = AvlTreeInsert(root,7);
    root = AvlTreeInsert(root,8);
    root = AvlTreeInsert(root,9);
    root = AvlTreeInsert(root,10);
    root = AvlTreeInsert(root,11);
    root = AvlTreeInsert(root,12);
    root = AvlTreeInsert(root,13);
    root = AvlTreeInsert(root,14);
    root = AvlTreeInsert(root,15);
    inOrderVisitUseRecur(root);
    return 0;
}