入门级神经网络之权重训练

写在前面的话

训练没有使用任何框架，最能靠近神经网络学习本质的一段微代码。之后会用tensorflow等框架来进行快速搭建。

另：我的博客更偏向于代码实现，关键难点自己的理解。如果要更基础的机器学习，这里有个楼主感觉写的不错：http://tieba.baidu.com/p/3013551686?pid=49703036815&see_lz=1#
这个楼主写的好像是采集了两家的教程，至少楼主的很多图片是从这两家教程中截屏的。这里我把教程链接也贴出来
① https://study.163.com/course/introduction/1004570029.html
② https://study.163.com/course/introduction/1003842018.html

本文代码参考：python.jobbole.com/82758

一、搭建二层神经网络

样本数据

代码全文

注：这段代码与参考代码有所出入，主要是添加了tensorboard功能

import numpy as np
import tensorflow as tf

# sigmoid function
def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x)
    return 1/(1+np.exp(-x))

# input dataset
X = np.array([  [0,0,1],
                [1,1,1],
                [1,0,1],
                [0,1,1] ])

# output dataset            
y = np.array([[0,1,1,0]]).T

# seed random numbers to make calculation
# deterministic (just a good practice)
np.random.seed(1)

# initialize weights randomly with mean 0
syn0 = tf.Variable(tf.zeros([3,1]))

#向tensorboard添加数据

tf.summary.histogram('syn0[0]',syn0[0])
tf.summary.histogram('syn0[1]',syn0[1])
tf.summary.histogram('syn0[2]',syn0[2])
#将所有的summary全部保存磁盘
merged = tf.summary.merge_all()

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

#tensorboard所需数据写入文件
writer = tf.summary.FileWriter('./tensorflow/',sess.graph)

for iter in range(600):
    # forward propagation
    l0 = X
    l1 = nonlin(np.dot(l0,sess.run(syn0)))

    # how much did we miss?
    l1_error = y - l1

    # multiply how much we missed by the 
    # slope of the sigmoid at the values in l1
    l1_delta = l1_error * nonlin(l1,True)

    # update weights
    sess.run(tf.assign(syn0,  sess.run(syn0) + np.dot(l0.T,l1_delta)))

    #向tensorboard添加数据
    rs = sess.run(merged)
    writer.add_summary(rs,iter)
    
print("Output After Training:")
print(l1)

打印结果

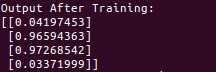
观察tensorboard

相比原参考链接，我们这里添加了tersorboard功能，用以查看权重值syn0变化趋势，我这里训练了600次，可以看到曲线还没有达到 ‘完美’ ，说明需要继续训练。

注：更为详尽的tensorboard代码实现参考链接：https://www.cnblogs.com/maskerk/p/9973664.html

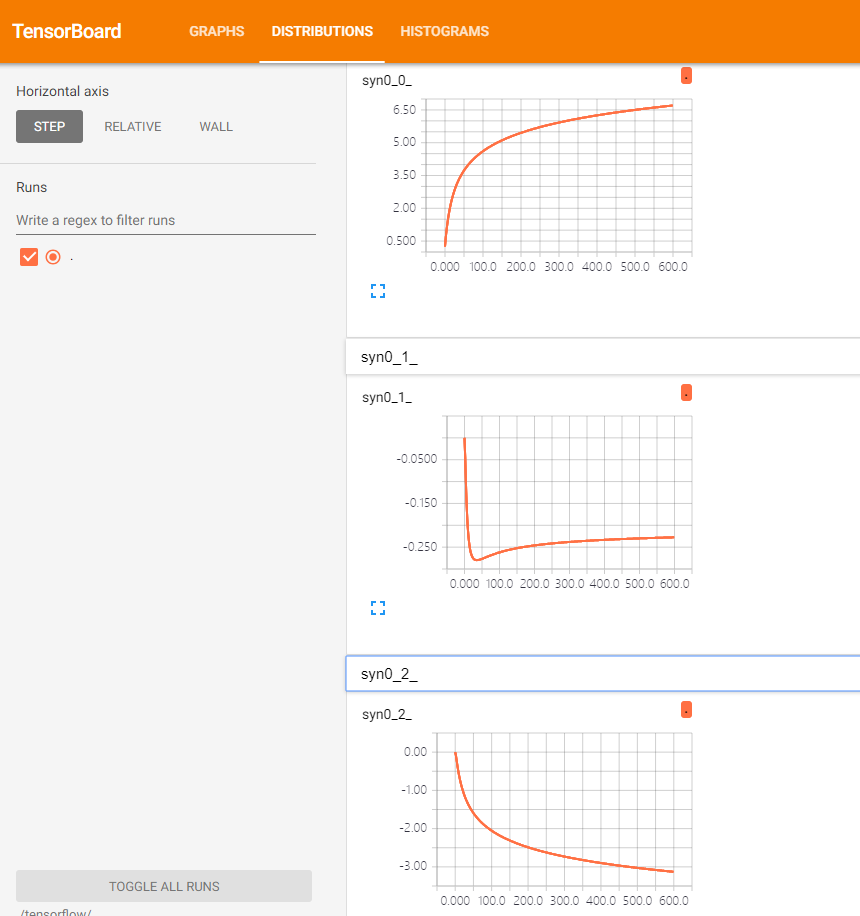
额外解析

为什么叫额外解析呢，我这里只说我认为比较关键的地方，与原作者形成补充。

• 1.从训练数据这里看起，l0为输入层，l1为输出层，这里只有两层，就没有隐藏层了。

• 2.首先，这里l0点乘syn0(权重系数)得到l1，这里就像线性方程 l1 = syn0*l0(y = W * x) 。然后把相乘的结果送入nonlin 函数，这个函数就是激活函数 ，在激活函数中执行 1/(1+np.exp(-x))，这样执行的后果是什么呢？就是不管你之前送进去的值是多少，现在出来的结果都是0~1之间了。函数图像如下图。
  

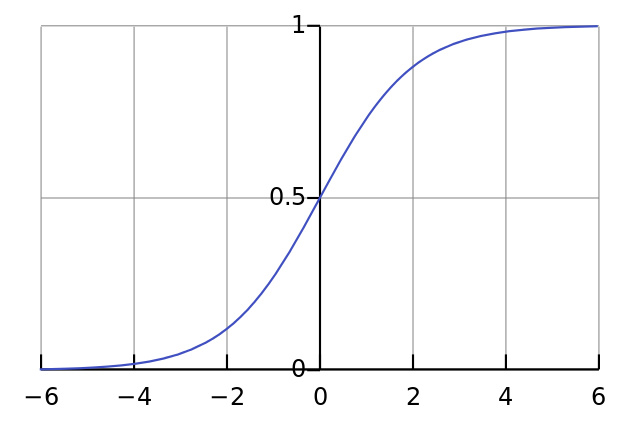
其实这样 l1 就得到了，也就是结果，但这是训练的第一次的第一步，基本上距离正确结果很远(除非中彩)。

• 3. l1_error = y - l1
  然后计算误差，我们知道要么是1要么是0，l1 的结果又在0~1之间，所以如果样本值为1 ， 1 - l1 的值为正值 ，样本值如果为0 ， 0 - l1的值为负值，这样，下一步l1 应该向左走还是向右走，就有方向 了。

• 4. l1_delta = l1_error * nonlin(l1,True)
  这里计算的 l1_delta ，实际上就是l1_error 乘上一个变化系数，这里的变化系数就是函数sigmoid 的斜率，从函数的图像可以看到，y轴在0.5处斜率最大，靠近0或者1斜率也会逐渐变小，这里乘上这个斜率，能够使得预测值在距离0或者1较远时能尽快向0或1靠拢。同时斜率一直为正数，这样相乘不会影响我们上一段说的变化方向。

• 5.syn0 += np.dot(l0.T,l1_delta)
  这里学习的过程，其实就是不断修改权重系数syn0 使其不断靠近正确值得过程。这里l0.T*l1_delta，这样就是每一列中的元素去乘l1_delta ，这样就是第一列的元素分别乘以误差然后相加，表现的是每一列与误差的关系。其实仔细看一下就能发现，我们的第一列的数值和最终结果是相符合的。

二、搭建三层神经网络

样本数据

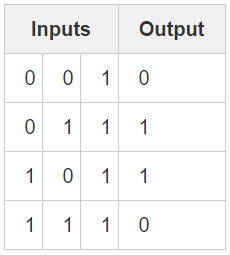
代码全文

import numpy as np

def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x)

    return 1/(1+np.exp(-x))

X = np.array([[0,0,1],
            [0,1,1],
            [1,0,1],
            [1,1,1]])

y = np.array([[0],
            [1],
            [1],
            [0]])

np.random.seed(1)

# randomly initialize our weights with mean 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1

for j in xrange(60000):

    # Feed forward through layers 0, 1, and 2
    l0 = X
    l1 = nonlin(np.dot(l0,syn0))
    l2 = nonlin(np.dot(l1,syn1))

    # how much did we miss the target value?
    l2_error = y - l2

    if (j% 10000) == 0:
        print "Error:" + str(np.mean(np.abs(l2_error)))

    # in what direction is the target value?
    # were we really sure? if so, don't change too much.
    l2_delta = l2_error*nonlin(l2,deriv=True)

    # how much did each l1 value contribute to the l2 error (according to the weights)?
    l1_error = l2_delta.dot(syn1.T)

    # in what direction is the target l1?
    # were we really sure? if so, don't change too much.
    l1_delta = l1_error * nonlin(l1,deriv=True)

    syn1 += l1.T.dot(l2_delta)
    syn0 += l0.T.dot(l1_delta)

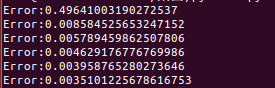
打印结果

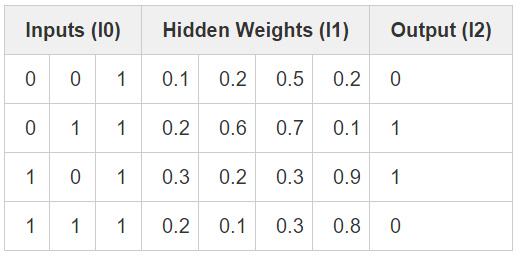
隐藏层示例

额外解析

---

① 这里首先一个问题就是，输出结果不是和某一列直接相关了 ，这是和第一个demo最大的差别。这里的输出值为第一列与第二列的异或运算 。这里使用了三层神经网络，即 l0输入层， l1 隐藏层，l2 输出层

---

② 这里将 syn0 定义为 三行四列，这里我没懂 为什么，这也是一个关键的地方。如果之后弄明白了再回来补充。
syn1 定义为四行一列很明白，就是为了数据结果是为了四行一列。

---

③

     l1 = nonlin(np.dot(l0,syn0))
     l2 = nonlin(np.dot(l1,syn1))

这里是前向传递 。输入层 * 权重0 得到隐藏层， 隐藏层 * 权重1 得到输出层，没什么好说的

---

④

l2_error = y - l2
l2_delta = l2_error*nonlin(l2,deriv=True)
l1_error = l2_delta.dot(syn1.T)
l1_delta = l1_error * nonlin(l1,deriv=True)

syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)

这里是反向传递 ,计算误差然后从输出层传递回输入层。

第一步。l2误差为样本值-输出层值，l2_delta = l2的计算误差方式与第一个demo的l1计算误差方式相同。

第二步。方式和第一个demo也相同。 l2(输出层)的误差 * 变化系数(激励函数的导数值)

第三步。这里就开始不同了。l1(隐藏层)的误差 = l2_delta * l1层的权重系数。按照惯例，是 l1 - l1样本值，但是这里没有样本值，l2的输出误差又和l1的权重系数有直接联系，所以这里就用了这么个式子，用以钳制 l1权重值。

第四步。方式和第二步类似。

第五步。因为是反向传递，所以权重值在修改的时候，先改的后边的权重值syn1 += l1.T.dot(l2_delta)

迭代循环

思考

代码中没有提到学习效率，我个人思考，这里的学习效率就是函数 sigmoid 的斜率。或者delta再乘以一个数值，这里默认了为1，所以没有再乘。