CART分类树算法
特征选择
我们知道,在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益比来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢?有!CART分类树算法使用基尼系数 \(^{[ 1 ]}\)来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。
连续特征和离散值处理
对于CART分类树连续值的处理问题,其思想和C4.5是相同的,都是将连续的特征离散化。唯一的区别在于在选择划分点时的度量方式不同,C4.5使用的是信息增益比,则CART分类树使用的是基尼系数。
比如 \(m\) 个样本的连续特征 \(A\) 有 \(m\) 个,从小到大排列为\(a_1,a_2,...,a_m\),则CART取相邻两样本值的平均数,一共取得 \(m-1\) 个划分点,其中第 \(i\) 个划分点 \(T_i\) 表示为:\(T_i= \frac{a_i+a_{i+1}}{2}\) 。对于这 \(m-1\) 个点,分别计算以该点作为二元分类点时的基尼系数。选择基尼系数最小的点作为该连续特征的二元离散分类点。比如取到的基尼系数最小的点为 \(a_t\) ,则小于 \(a_t\) 的值为类别 \(1\),大于 \(a_t\) 的值为类别 \(2\),这样我们就做到了连续特征的离散化。要注意的是,与ID3或者C4.5处理离散属性不同的是,如果当前节点为连续属性,则该属性后面还可以参与子节点的产生选择过程。
对于CART分类树离散值的处理问题,采用的思路是不停的二分离散特征。
回忆下ID3或者C4.5,如果某个特征A被选取建立决策树节点,如果它有\(A1,A2,A3\)三种类别,我们会在决策树上一下建立一个三叉的节点。这样导致决策树是多叉树。但是CART分类树使用的方法不同,他采用的是不停的二分,还是这个例子,CART分类树会考虑把 \(A\) 分成\(\{{A1}\}\)和\(\{{A2,A3}\},\{{A2}\}\)和\(\{{A1,A3\}}, \{{A3}\}和\)\(\{{A1,A2}\}\)三种情况,找到基尼系数最小的组合。
建立CART分类树
算法输入是训练集\(D\),基尼系数的阈值,样本个数阈值。
输出是决策树T。
我们的算法从根节点开始,用训练集递归的建立CART树。
- 对于当前节点的数据集为 \(D\),如果样本个数小于阈值或者没有特征,则返回决策子树,当前节点停止递归。
- 计算样本集\(D\)的基尼系数,如果基尼系数小于阈值,则返回决策树子树,当前节点停止递归。
- 计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数,对于离散值和连续值的处理方法和基尼系数的计算见第二节。缺失值的处理方法和上篇的C4.5算法里描述的相同。
- 在计算出来的各个特征的各个特征值对数据集\(D\)的基尼系数中,选择基尼系数最小的特征A和对应的特征值\(a\)。根据这个最优特征和最优特征值,把数据集划分成两部分\(D_1\)和\(D_2\),同时建立当前节点的左右节点,做节点的数据集\(D\)为\(D_1\),右节点的数据集\(D\)为\(D_2\).
- 对左右的子节点递归的调用1-4步,生成决策树。
对于生成的决策树做预测的时候,假如测试集里的样本A落到了某个叶子节点,而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。
建立CART回归树
CART回归树和CART分类树的建立算法大部分是类似的,所以这里我们只讨论CART回归树和CART分类树的建立算法不同的地方。
首先,我们要明白,什么是回归树,什么是分类树。两者的区别在于样本输出,如果样本输出是离散值,那么这是一颗分类树。如果果样本输出是连续值,那么那么这是一颗回归树。
除了概念的不同,CART回归树和CART分类树的建立和预测的区别主要有下面两点:
- 连续值的处理方法不同
- 决策树建立后做预测的方式不同。
对于连续值的处理,我们知道CART分类树采用的是用基尼系数的大小来度量特征的各个划分点的优劣情况。这比较适合分类模型,但是对于回归模型,我们使用了常见的和方差的度量方式,CART回归树的度量目标是,对于任意划分特征 \(A\),对应的任意划分点 \(s\) 两边划分成的数据集 \(D_1\)和 \(D_2\),求出使 \(D_1\) 和 \(D_2\) 各自集合的均方差最小,同时 \(D_1\) 和 \(D_2\) 的均方差之和最小所对应的特征和特征值划分点。表达式为:
其中,\(c_1\) 为 \(D_1\) 数据集的样本输出均值,\(c_2\) 为 \(D_2\) 数据集的样本输出均值。
对于决策树建立后做预测的方式,上面讲到了CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别,它采用的是用最终叶子的均值或者中位数来预测输出结果。
除了上面提到了以外,CART回归树和CART分类树的建立算法和预测没有什么区别。
[1] 基尼系数 :数据集 \(D\) 的纯度可以用基尼值来度量,
其中, \(p(x_i)\) 是分类 \(x_i\) 出现的概率, \(n\) 是分类的数目。\(Gini(D)\) 反映从数据集 \(D\) 中随机抽取两个样本,其类别标记不一致的概率。因此,\(Gini(D)\) 越小,则数据集 \(D\) 的纯度越高。
果是二类分类问题,计算就更加简单了,如果属于第一个样本输出的概率是 \(p\),则基尼系数的表达式为:
对于个给定的样本 \(D\) ,假设有 \(K\) 个类别, 第 \(k\) 个类别的数量为 \(C_k\),则样本$ D$ 的基尼系数表达式为:
特别的,对于样本 \(D\),如果根据特征 \(A\) 的某个值 \(a\) ,把 \(D\) 分成$ D_1$和 \(D_2\)两部分,则在特征 \(A\) 的条件下,$ D$ 的基尼系数表达式为:
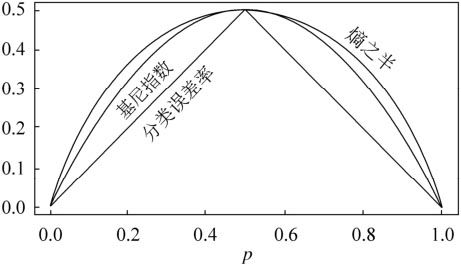
大家可以比较下基尼系数表达式和熵模型的表达式,二次运算是不是比对数简单很多?尤其是二类分类的计算,更加简单。但是简单归简单,和熵模型的度量方式比,基尼系数对应的误差有多大呢?对于二类分类,基尼系数和熵之半的曲线如下:
参考资料
[1] Yolanda. 决策树算法--CART分类树算法 [EB/OL] 知乎
[2] 刘建平.决策树算法原理(下) [EB/OL] 博客园