(2012新课标9)已知$omega>0,$函数$f(x)=sin(omega x+dfrac{pi}{4})$在$(dfrac{pi}{2},pi)$上单调递减,则$omega$的取值范围是______

分析:
常规方法:$dfrac{pi}{2}+2kpileomega x+dfrac{pi}{4}ledfrac{3pi}{2}+2kpi,kin Z$
得$xin[dfrac{pi+8kpi}{4omega},dfrac{5pi+8kpi}{4omega}]$取$k=0$得$dfrac{pi}{4omega}ledfrac{pi}{2},dfrac{5pi}{4omega}gepi$得$omegain[dfrac{1}{2},dfrac{5}{4}]$
巧法:利用图像伸缩变换,如图
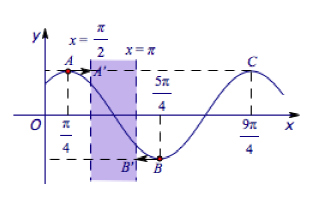
先对函数$f(x)=sin(x+dfrac{pi}{4})$作图,$f(x)=sin(omega x+dfrac{pi}{4})$是由上图纵坐标不变,横坐标伸缩为原来的$dfrac{1}{omega}$所得.
考虑$dfrac{pi}{4omega}=dfrac{pi}{2},dfrac{5pi}{4omega}=pi$易得$omegain[dfrac{1}{2},dfrac{5}{4}]$