已知函数$f(x)=e^x-e^{-x}-2x$
(1)讨论$f(x)$的单调性;
(2)设$g(x)=f(2x)-4bf(x),$当$x>0$时,$g(x)>0,$求$b$的最大值;
(3)已知$1.4142<sqrt{2}<1.4143$,估计$ln 2$的近似值(精确到0.001).

分析:(1)$f^{'}(x)=e^x+e^{-x}-2ge2sqrt{e^xcdot e^{-x}}-2=0$,故$f(x)$在$R$上单调递增.
(2)$g(x)=e^{2x}-e^{-2x}-4x-4b(e^x-e^{-x}-2x),$
$g^{'}(x)=2e^{2x}+2e^{-2x}-4-4b(e^x+e^{-x}-2)=2(e^x+e^{-x}-2)(e^x+e^{-x}+2-2b)$,
设$h(x)=e^x+e^{-x}+2-2b,h(0)=4-2b$
当$ble 2$时,易知$h(x)ge h(0)=0,$故$g(x)$在$(0,+infty)$上单调递增,由$g(0)=0$知,$g(x)>0$,满足题意.
当$b>2$时,存在零点$phi$,使得$h(phi)=0,phi=ln(b-1+sqrt{b^2-2b})$,故$g(x)$在$(0,phi)$单调递减,又$g(0)=0,$故$g(x)<0$,不符合题意.
综上,$b$的最大值为2.
(3)首先应该要知道$ln 2$的大概值为0.693(平时的积累,类似要知道$piapprox3.1415926$.)这里选择的函数应该是带有$b$的$g(x)$ 而不是$f(x)$, 其次要估计$ln 2$ 又要用到$sqrt{2}$, 由$g(x)$ 的函数形式,$x$ 的取值很容易尝试$lnsqrt{2},g(lnsqrt{2})=(4b-2)ln2+dfrac{3}{2}-2sqrt{2}b$, 当$bin(dfrac{1}{2},2]$ 时 由$g(lnsqrt{2})>0$ 得$ln 2>dfrac{2sqrt{2}b-dfrac{3}{2}}{4b-2}gedfrac{8sqrt{2}-3}{12}>0.6928$
上界尝试在当$b>2$时估计.令$phi=ln2$,此时$b=dfrac{3sqrt{2}}{4}+1$,由(2)知$g(lnsqrt{2})<g(0)=0,$ 得
$ln 2<dfrac{2sqrt{2}b-dfrac{3}{2}}{4b-2}=dfrac{18+sqrt{2}}{28}<0.6934.$
故$ln2approx 0.693$
练习:

附解答:




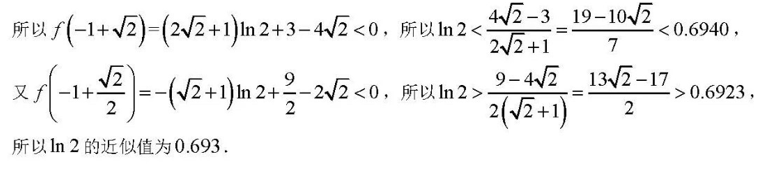
注:泰勒展开$ln(1+x)=x-dfrac{x^2}{2}+dfrac{x^3}{3}-cdots+(-1)^{n-1}dfrac{x^n}{n}+o(x^n)$
故$ln(dfrac{1+x}{1-x})=2(x+dfrac{x^3}{3}+cdots)$取$x=dfrac{1}{3}$则$ln(2)approx 0.693$