MT【308】投影的定义

已知向量$overrightarrow{a},overrightarrow{b}$满足:$|overrightarrow{a}|=2$,向量$overrightarrow{b}$与$overrightarrow{a}-overrightarrow{b}$夹角为$dfrac{2pi}{3}$
则$overrightarrow{a}cdot overrightarrow{b}$的取值范围_____

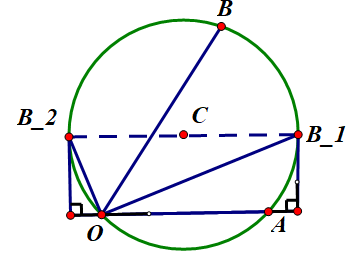
提示:如图记$overrightarrow{a}=overrightarrow{OA},overrightarrow{b}=overrightarrow{OB}$
$overrightarrow{OA}cdotoverrightarrow{OB}=|OA||OB|cosangle AOB=2|OB|cosangle AOB$由投影的几何意义知,当点$B$运动到$B_1,B_2$时分别取到最大和最小,易得$overrightarrow{a}cdot overrightarrow{b}in[2-dfrac{4sqrt{3}}{3},2+dfrac{4sqrt{3}}{3}]$

练习:已知$|overrightarrow{e}|=|overrightarrow{a}+overrightarrow{e}|=|overrightarrow{b}-overrightarrow{e}|=1$
求$overrightarrow{a}cdotoverrightarrow{b}$的取值范围_____

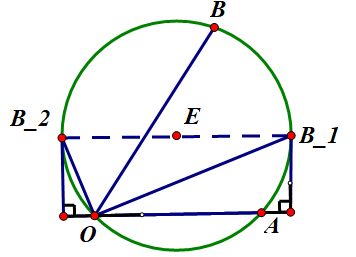
提示:如图单位圆中设$-overrightarrow{a}=overrightarrow{OA},overrightarrow{b}=overrightarrow{OB},overrightarrow{e}=overrightarrow{OE}$

$|OA|=2x,xin[0,1]$
$(overrightarrow{OA}cdotoverrightarrow{OB})_{max}=overrightarrow{OA}cdotoverrightarrow{OB_1}=2x(1+x)le4$
$(overrightarrow{OA}cdotoverrightarrow{OB})_{min}=overrightarrow{OA}cdotoverrightarrow{OB_2}=2x(x-1)ge-dfrac{1}{2}$
故:$overrightarrow{a}cdotoverrightarrow{b}in[-4,dfrac{1}{2}]$

练习：已知$2|overrightarrow{a}|=|overrightarrow{b}|=|overrightarrow{c}|=1$,则$(overrightarrow{c}-overrightarrow{a})cdot(overrightarrow{c}-overrightarrow{b})$的取值范围为______

答案：$[-dfrac{1}{8},3]$，提示：方法如上面的练习题