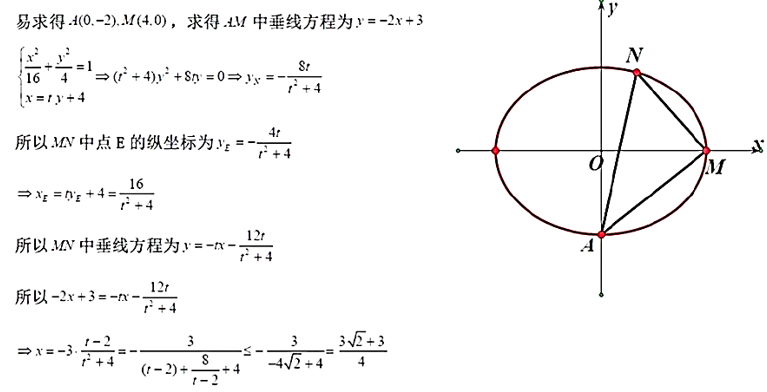
已知椭圆$dfrac{x^2}{16}+dfrac{y^2}{4}=1$的下顶点为$A$,若直线$x=ty+4$与椭圆交于不同的两点$M,N$则当$t=$______时,$Delta AMN$外心的横坐标最大.

解答:设椭圆与圆交于四个点$A,M,N,T$,其中$M(4,0)$
则$NTcup AM:(Ax+By+C)*(x-2y-4)=0$则两条直线与椭圆构成的曲线系$(Ax+By+C)*(x-2y-4)+lambda(dfrac{x^2}{16}+dfrac{y^2}{4}-1)=0$由于圆的方程要求$xy$项没有,且$x^2,y^2$前系数相同.
故$(x+2y+C)*(x-2y-4)+lambda(dfrac{x^2}{16}+dfrac{y^2}{4}-1)=0$且$1+dfrac{lambda}{16}=-4+dfrac{lambda}{4}=0,$
得$lambda=dfrac{80}{3}$从而圆心的横坐标为$dfrac{3}{16}(4-C)$ 因为直线$NT:x+2y+C=0$
与椭圆$dfrac{x^2}{16}+dfrac{y^2}{4}=1$相交.故$1^2*16+2^2*4-C^2ge0$ 即$-4sqrt{2}le Cle4sqrt{2}$
故圆心横坐标最大为$dfrac{3+3sqrt{2}}{4}$当$C=-4sqrt{2}$此时$N=T(2sqrt{2},sqrt{2})$代入$x=ty+4$
得$t=2-2sqrt{2}$
常规方法: