排序算法的稳定性:
假设有一串数据:(4,1)(3,1)(3,7)(5,6);要求按照第一个数排序,结果如下:
第一种:(3,1)(3,7)(4,1)(5,6)(3相同,维持原来的次序)
第二种:(3,7)(3,1)(4,1)(5,6)(3相同,次序被改变)
第一种是稳定的。
冒泡排序(以从小到大排为例):
每次走一遍把最大的元素冒泡,排到最后。
''' 冒泡排序:它也可以用于之前讲的链表什么的,只是交换部分稍微烦一点,思想一样。这里简单一点 ,以数字为例 ''' def bubble_sort(alist): '''冒泡排序,参数为列表''' n = len(alist)-1 for j in range(n): for i in range(n-j): if alist[i]>alist[i+1]: # 前一个大于后一个,交换 alist[i], alist[i+1] = alist[i+1], alist[i] # 这样写在python这种动态语言中可以 if __name__ == '__main__': a = [2,0,5,1,10] bubble_sort(a) print(a)
冒泡排序的时间复杂度为:最坏可以认为是O(n^2),稳定的
改进:假如传入的序列就是有序的,比如[1,2,3,4,5,6]。此时按照上面代码还是要一步步比较,复杂度是一样的。改进之后,最优时间复杂度为O(n),最坏时间复杂度不变。
def bubble_sort(alist): '''冒泡排序,参数为列表''' n = len(alist)-1 for j in range(n): count = 0 for i in range(n-j): if alist[i]>alist[i+1]: # 前一个大于后一个,交换 alist[i], alist[i+1] = alist[i+1], alist[i] # 这样写在python这种动态语言中可以 count += 1 if count == 0: return
选择排序:
思想解释:每次找到最小的值,与无序数中的一个数交换,比如:
a = [52,100,23,43,55,20,17,108]
找到最小值是17,将17与52交换,得:
a = [17,100,23,43,55,20,52,108]
看除了第一个数17外,其他最小的为20,与“第一个数”100交换:
a = [17,20,23,43,55,100,52,108]
此时,前面两个数已经有序,以此往下。
def select_sort(alist): """选择排序,既然是研究数据结构与算法,这里不用min()函数""" n = len(alist) for j in range(n-1): # 记录最小值的位置,这里首次默认是无序中的第一个 min_index = j for i in range(j+1,n): if alist[i]<alist[min_index]: min_index = i alist[j], alist[min_index] = alist[min_index], alist[j]
选择排序的时间复杂度:O(n^2),不稳定
插入排序算法:
思想理解,与上面选择排序有点雷士,其实还是将序列无形的分为两部分。比如序列[52,100,23,43,55,20,17,108]。
将序列分为[52, 100,23,43,55,20,17,108],第一部分是有序的。
然后将无序中的第一个100与有序中52比较,放在正确的位置[52,100, 23,43,55,20,17,108],
同理接着比较23与[52,100],将其插入正确的位置[23,52,100, 43,55,20,17,108]
注意:插入的过程其实就是一个小排序,比如插入23时,先与100比,然后与52........
def insert_sort(alist): """插入排序""" for j in range(1,len(alist)): i = j # 从无序部分选一个插入到有序部分的过程 while i>0: if alist[i]<alist[i-1]: alist[i], alist[i-1] = alist[i-1], alist[i] i -= 1 else: # 因为有序部分是有序的,只要前一个数比当前数小,那前面所有的数都比当前数小 break
最坏时间复杂度是O(n^2),最优时间复杂度是O(n),稳定的
希尔排序:
它其实就是插入排序的改进版,思想百度百科一下就可以了。
简单介绍:它有一个gap(间隙),假设gap=4。原序列为54,26,93,17,77,31,44,55,20;
因为gap=4,索引相差四的抽出,那原序列变成4层:
54, 77 , 20
26, 31,
93, 44
17 55
每一层排序后再插入回去,即经过第一次排序之后:20,26,44,17,54,31,93,55,77;
再取gap=2,原序列变成两层:
20 44 54 93 77
26 17 31 55
同理每层子序列用插入算法,再取gap=1.得到最后的结果。
def shell_sort(alist): """希尔排序,核心部分其实是插入排序""" n = len(alist) gap = n//2 # 其实有最优的gap值,这里直接用长度的一半取整 # gap变化为0前,插入算法执行的次数 while gap>=1: # 内层循环其实就是插入算法,与普通的插入算法的区别在于gap for j in range(gap,n): i = j while i>0: if alist[i]<alist[i-gap]: alist[i], alist[i-gap] = alist[i-gap], alist[i] i -= gap else: break gap //= 2
最坏时间复杂度O(n^2),最优时间复杂度根据gap值不同的而不同(优化问题)。不稳定
快速排序
具体思想介绍可以百度一下,其实有点像冒泡的改进。举个例子:
假设原序列为:54,26,93,17,77,31,44,55,20;
先找到第一个数54在有序情况下的位置,怎么找?设定两个游标,游标low先指向26,游标high先指向最后一个数20.
当low指向的数小于54时,可以继续向high的方向移动,否则先静止;同理当high指向的数大于54时可以向low的方向移动,否则静止;
按照上面的要求,此时54,26,93(low),17,77,31,44,55,20(high);
卡主不动了,这时候交换93,20的位置,数据变成54,26,20(low),17,77,31,44,55,93(high);这时不卡了,继续移动(先动low),一直到low与high重合,如下:
54, 26,20,17,31,44(low_and_high),77,55,93
此时确定54的位置:26,20,17,31,44, 54 ,77,55,93同理处理54前后两部分;
大致思想是这样,为了方便编程,稍微变通一下(仍然是快速排序):
序列还是上面那个,一开始low指向54,high指向20,设一个mid_value=54(把第一个数存起来),游标还是往中间动;
high先动,能动的条件一样,此时20,high游标不能动,就将20代替low指向的数(54早已存起来)。变成20(low),26,93,17,77,31,44,55,空(high);
这时候low动起来,一直到:20,26,93(low),17,77,31,44,55,空(high)
替换:20,26,空(low),17,77,31,44,55,93(high);high动
最终:20,26,44,17,31,空(low_high),77,55,93
让空=54,20,26,44,17,31, 54, 77,55,93,同理处理54两边。

1 def quick_sort(alist): 2 """快速排序,错误示范,错误的地方在下面递归""" 3 n = len(alist) 4 mid_value = alist[0] 5 low = 0 6 high = n-1 7 8 while low < high: 9 # high左移动(等于的情况放一边处理比较好) 10 while low < high and alist[high] >= mid_value: 11 high -= 1 12 alist[low] = alist[high] 13 # low右移 14 while low < high and alist[low] < mid_value: 15 low += 1 16 alist[high] = alist[low] 17 # 从while退出,low等于high 18 alist[low] = mid_value 19 20 # mid_walue两边处理方式与上面一样 21 quick_sort(alist[:low-1]) #不能切片传,这等于传一个新的列表了,也就是说操作的不是一个列表 22 quick_sort(alist[low+1:])
def quick_sort(alist, first, last): """ 快速排序 :param alist: 列表 :param first: 列表的第一个元素索引,0 :param last: 列表最后一个元素,len()-1 :return: """ # 递归的终止条件 if first >= last: return mid_value = alist[first] low = first high = last while low < high: # high左移动(等于的情况放一边处理比较好) while low < high and alist[high] >= mid_value: high -= 1 alist[low] = alist[high] # low右移 while low < high and alist[low] < mid_value: low += 1 alist[high] = alist[low] # 从while退出,low等于high alist[low] = mid_value # mid_walue两边处理方式与上面一样 quick_sort(alist, first, low-1) quick_sort(alist, low+1, last) if __name__ == '__main__': b = [54,26,93,17,77,31,44,55,20] quick_sort(b,0,len(b)-1) print(b)
快速排序的最优时间复杂度O(nlogn),最坏时间复杂度O(n^2),不稳定。
归并排序:
思想:百度一下就好
def Merge_Sort(lists): if len(lists) <= 1: return lists mid = int(len(lists) / 2) # left 采用归并排序后形成的有序的新的列表 left = Merge_Sort(lists[:mid]) # right 采用归并排序后形成的有序的新的列表 right = Merge_Sort(lists[mid:]) # 将两个有序的子序列合并 # Merge(left, right) r, l=0, 0 # 为两个指针 result=[] while l<len(left) and r<len(right): if left[l] < right[r]: result.append(left[l]) l += 1 else: result.append(right[r]) r += 1 result += list(left[l:]) result += list(right[r:]) return result if __name__ == '__main__': b = [54,26,93,17,77,31,44,55,20] b = Merge_Sort(b) print(b)
上面代码递归有点复杂,执行流程可看https://www.bilibili.com/video/av21540971/?p=35
最坏与最优时间复杂度都是:O(nlogn),稳定。
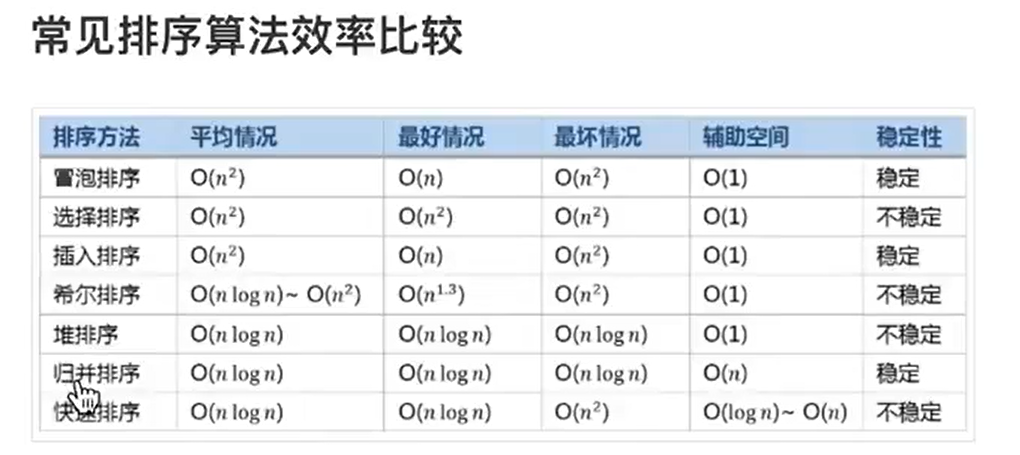
堆排序没介绍,可以百度一下,快速排序用的比较多。
