排序算法——堆排序
http://www.cnblogs.com/luchen927/archive/2012/03/08/2381446.html
前一阵子一直在写排序的系列文章,最近因为一些事情耽搁了几天,也穿插了几篇其他类别的随笔。今天还是回到排序上面来,善始善终,呵呵。
今天要介绍的也是一种效率很高的排序——堆排序
思想
堆排序,顾名思义,就是基于堆。因此先来介绍一下堆的概念。
堆分为最大堆和最小堆,其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子,最小堆要求节点元素都小于其左右孩子,两者对左右孩子的大小关系不做任何要求,其实很好理解。有了上面的定义,我们可以得知,处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点,每次都取堆顶的元素,将其放在序列最后面,然后将剩余的元素重新调整为最大堆,依次类推,最终得到排序的序列。
或者说,堆排序将所有的待排序数据分为两部分,无序区和有序区。无序区也就是前面的最大堆数据,有序区是每次将堆顶元素放到最后排列而成的序列。每一次堆排序过程都是有序区元素个数增加,无序区元素个数减少的过程。当无序区元素个数为1时,堆排序就完成了。
本质上讲,堆排序是一种选择排序,每次都选择堆中最大的元素进行排序。只不过堆排序选择元素的方法更为先进,时间复杂度更低,效率更高。
图例说明一下:(图片来自http://www.cnblogs.com/zabery/archive/2011/07/26/2117103.html)

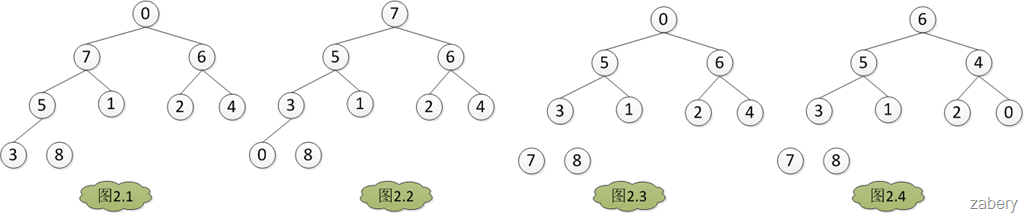
具体步骤如下:
1 首先从第一个非叶子节点开始,比较当前节点和其孩子节点,将最大的元素放在当前节点,交换当前节点和最大节点元素。
2 将当前元素前面所有的元素都进行1的过程,这样就生成了最大堆
3 将堆顶元素和最后一个元素交换,列表长度减1。由此无序区减1,有序区加1
4 剩余元素重新调整建堆
5 继续3和4,直到所有元素都完成排序
代码
int adjust_heap(vector<int> &v, int length, int i){
int left = 2 * i;
int right = 2 * i + 1;
int largest = i;
int temp;
while(left < length || right < length){
if (left < length && v[largest] < v[left]){
largest = left;
}
if (right < length && v[largest] < v[right]){
largest = right;
}
if (i != largest){
temp = v[largest];
v[largest] = v[i];
v[i] = temp;
i = largest;
left = 2 * i;
right = 2 * i + 1;
}
else{
break;
}
}
}
int build_heap(vector<int> &v, int length){
int i;
int begin = length/2 - 1; //get the last parent node
for (i = begin; i>=0; i--){
adjust_heap(v,length,i);
}
}
int heap_sort(vector<int> &v){
int length = v.size();
int temp;
printline("before sort:",v);
build_heap(v,length);
while(length > 1){
temp = v[length-1];
v[length-1] = v[0];
v[0] = temp;
length--;
adjust_heap(v,length,0);
}
printline("after sort:",v);
}
分析
堆排序的平均时间复杂度为O(nlogn),接近于最坏的时间复杂度。在最好情况下,时间复杂度为O(1).
