当概率模型依赖于无法观测的隐性变量时,使用普通的极大似然估计法无法估计出概率模型中参数。此时需要利用优化的极大似然估计:EM算法。
在这里我只是想要使用这个EM算法估计混合高斯模型中的参数。由于直观原因,采用一维高斯分布。
一维高斯分布的概率密度函数表示为:
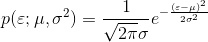
多个高斯分布叠加在一起形成混合高斯分布:
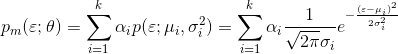
其中:k 表示一共有 k 个子分布,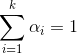 。为什么累加之和为 1?因为哪怕是混合模型也表示一个概率密度,从负无穷到正无穷积分概率为 1,所以只有累加之和为 1才能保证,很简单的推导。
。为什么累加之和为 1?因为哪怕是混合模型也表示一个概率密度,从负无穷到正无穷积分概率为 1,所以只有累加之和为 1才能保证,很简单的推导。
设总体 ξ,总体服从混合高斯分布。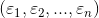 是一个取自总体的样本。罢了,公式编辑实在慢到令人发指,简单记录而已,手写。
是一个取自总体的样本。罢了,公式编辑实在慢到令人发指,简单记录而已,手写。
以下是关于一维混合高斯分布的参数估计推导过程:


参考:周志华《机器学习》
简单代码实现一下,代码很丑:

import numpy as np import matplotlib.pyplot as plt # 使用 numpy 生成两组符合高斯分布(正态分布)的数据,然后将他们累加成混合模型,使用 EM 算法求解其中参数 # 假设两个分布累加的系数 α1=0.6,α2=0.4 # 假设 N1 分布的均值 μ1=1.7,方差 δ1²=0.57²=0.3249 # 假设 N2 分布的均值 μ2=3.5,方差 δ2²=0.33²=0.1089 np.random.seed(77) num1 = 6000 num2 = 4000 X1 = np.random.normal(1.7, 0.57, num1).astype(np.float32) X2 = np.random.normal(3.5, 0.33, num2).astype(np.float32) X = np.hstack((X1, X2)) # 其中包含两个高斯分布的数据 np.random.shuffle(X) # 混洗数据 re_tuple = plt.hist(X, 300, density=1, facecolor='r') plt.show() # 设置 EM 算法的初始值,任意设置 modulus = np.array([0.2, 0.8]) mean = np.array([1.1, 2.1]) var = np.array([1.2, 1.5]) # 首先计算每个样本点由每一个独立分布产生的概率,然后通过推导公式去更新参数 gamma_j_i = np.zeros((2, num1 + num2), dtype=np.float32) # 设置迭代次数 epochs = 100 for epoch in range(epochs): print('开始第 %d 次迭代 ...' % (epoch + 1)) # E 步 part_1 = 1 / np.sqrt(2 * np.pi * var[0]) part_2 = 1 / np.sqrt(2 * np.pi * var[1]) for i in range(2): part_i = 1 / np.sqrt(2 * np.pi * var[i]) for j in range(num1 + num2): p_m = (modulus[0] * (part_1 * np.exp(-1 * ((X[j] - mean[0]) ** 2) / (2 * var[0]))) + modulus[1] * (part_2 * np.exp(-1 * ((X[j] - mean[1]) ** 2) / (2 * var[1])))) p_i = modulus[i] * (part_i * np.exp(-1 * ((X[j] - mean[i]) ** 2) / (2 * var[i]))) gamma_j_i[i, j] = p_i / p_m # 中间计算步骤 sum_gamma_j_i = np.sum(gamma_j_i, axis=1) sum_for_mean = np.matmul(gamma_j_i, X) sum_for_var = np.sum(gamma_j_i * np.square(np.broadcast_to(X, (2, num1 + num2)) - mean.reshape((2, 1))), axis=1) # M 步 for i in range(2): mean[i] = sum_for_mean[i] / sum_gamma_j_i[i] modulus[i] = sum_gamma_j_i[i] / (num1 + num2) var[i] = sum_for_var[i] / sum_gamma_j_i[i] print('迭代 %d 次后得到的 N1 分布的比率、均值和方差分别为:%s %s %s' % (epoch + 1, modulus[0], mean[0], var[0])) print('迭代 %d 次后得到的 N2 分布的比率、均值和方差分别为:%s %s %s' % (epoch + 1, modulus[1], mean[1], var[1])) print() # 迭代 100 次后得到的结果是: # N1: 0.59798 1.69166 0.33037 # N2: 0.40202 3.49959 0.11023 # 总之,结果还不错
