斜率优化dp（[HNOI2008]玩具装箱）

斜率优化（凸壳优化）可应用于优化以下dp方程：

(dp(i) = max/min(dp(j) - g(i) cdot h(j))qquad 0leq j < i) 且 (g(i),h(j)) 递增。

通过斜率优化，可以将暴力的 (O(n^2)) 优化为 (O(n))。

具体步骤：

首先将min和max去掉，移项，可以得到以下方程：

[egin{aligned} dp(j) = g(i) cdot h(j) + dp(i) end{aligned} ]

其形状如直线的斜截式，因此可以令 (y = dp(j), k = g(i), x = h(j), b = dp(i))，原式转化为：

[egin{aligned} y = k cdot x + b end{aligned} ]

对于一个i，k是已知的，我们的目标就是求截距b的最大值或者最小值。

显然，对于所有的j，其dp(j)和h(j)都是已知的，分别对应x, y，我们可以将其看成平面坐标系上的一些点(P_j(h(j), dp(j)))。

对于一个i，问题转化为求所有过任一(P_j)的斜率为g(i)的直线的最小斜率。
如下图：

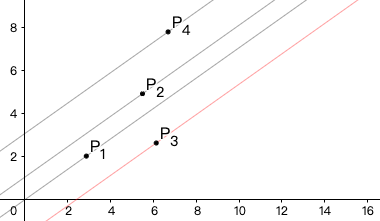
dp(i)即为经过(P_3)的直线的斜率。

如何找这个最下面的点？我们需要用单调队列维护下凸壳。如下图：

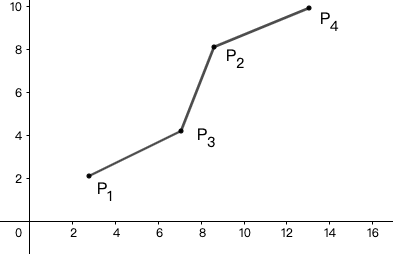
不断往队尾插入新的点，同时维护队列中相邻点构成的直线斜率是递增的，若遇到下降的斜率，就把队尾弹掉，例如当前队列最后两个点分别是(P_2, P_3)当插入(P_4)时，(P_3, P_2)的斜率比(P_2, P_4)大，于是把(P_2)弹掉，变为下图：

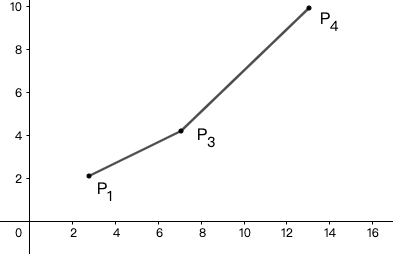
让一斜率为g(i)的直线从下方靠近，遇到第一个点时，情况如图：

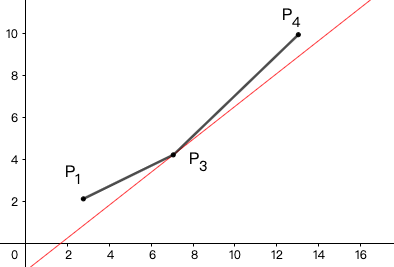
于是我们可以不断弹出队首，直到出现队首和下一个点构成的斜率大于g(i)，如上图(P_3)就是我们要求的答案点。

如何做到 (O(n)) 求出所有dp(i)？注意最开始一个性质：(g(i),h(j)) 递增，即x和要求的直线的斜率是递增的，我们不用对于每一个i跑一遍单调队列，只用跑一遍，i+1的答案点一定位于i的答案点之后。

实现(伪代码)：

//slope(i, j)表示点i, j连线的直线斜率
for(int i = 1; i <= n; i++) {
	while(head < tail && slope(q[head], q[head + 1]) < k(i)) ++head;//维护答案点
	int j = q[head]; //j即为当前i的答案点。
	update(dp[i]); //更新dp(i)
	while(head < tail && slope(q[tail - 1], q[tail]) > slope(q[tail], i)) --tail;//维护下凸壳
	q[++tail] = i; //入队
}

---

例题：[HNOI2008]玩具装箱

易得状态转移方程为：

[egin{aligned} f(i) = min(f(j) + (sum_i - sum_j + i - j - L - 1) ^ 2) end{aligned} ]

令：(g(i) = sum_i + i - L,quad h(j) = sum_j + j + 1)

拆掉min可得：

[egin{eqnarray*} f(i) = f(j) + g^2(i) + h^2(j) - 2 cdot g(i)cdot h(j)\ f(j) + h^2(j) = 2 cdot g(i)cdot h(j) + f(i) - g^2(i) end{eqnarray*} ]

即 (y = f(j) + h^2(j),quad x = h(j),quad k = 2 cdot g(i),quad b = f(i) - g^2(i))

接下来就可以写了。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long lld;
const int N = 50005;
int n, L, q[N << 1], head, tail;
lld sum[N], f[N];

lld y(int p) {
	return f[p] + (sum[p] + p + 1) * (sum[p] + p + 1);
}
lld k(int p) {
	return (sum[p] + p - L) * 2;
}
lld x(int p) {
	return sum[p] + p + 1;
}
double slope(int i, int j) {
	return (y(i) - y(j)) / (x(i) - x(j));
}
int main() {
	scanf("%d%d", &n, &L);
	for(int i = 1, p; i <= n; i++) {
		scanf("%d", &p);
		sum[i] = sum[i - 1] + p;
	}
	for(int i = 1; i <= n; i++) {
		while(head < tail && slope(q[head], q[head + 1]) < double(k(i))) ++head;
		int j = q[head];
		lld b = y(j) - k(i) * x(j);
		f[i] = b + (sum[i] + i - L) * (sum[i] + i - L);
		while(head < tail && slope(q[tail - 1], q[tail]) > slope(q[tail], i)) --tail;
		q[++tail] = i;
	}
	printf("%lld", f[n]);
	return 0;
}