题意
https://www.luogu.com.cn/problem/P2260
思路
具体思路见下图:
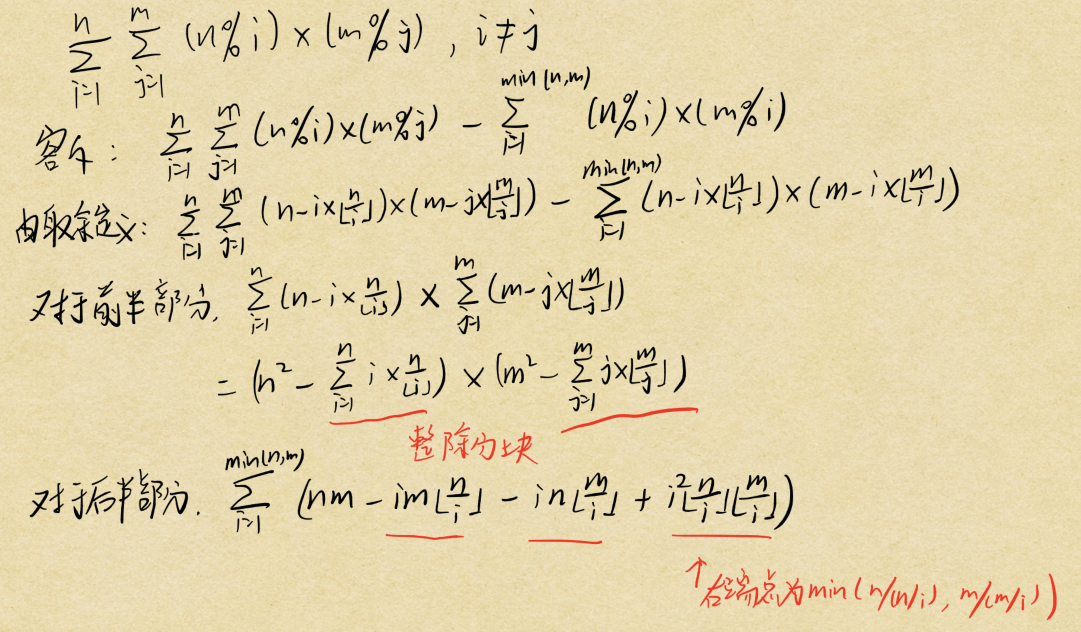
注意这个模数不是质数,不能用快速幂来求逆元,要用扩展gcd。
代码
#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
const int N=200005;
const int mod=19940417;
const double eps=1e-8;
const double PI = acos(-1.0);
#define lowbit(x) (x&(-x))
ll inv2,inv6,y;
void exgcd(ll a, ll b, ll& x, ll& y)
{
if (b == 0)
{
x = 1, y = 0;
return;
}
exgcd(b, a % b, y, x);
y -= a / b * x;
}
ll s(ll x)
{
return x%mod*(x+1)%mod*(2*x+1)%mod*inv6%mod;
}
ll f(ll x,ll mx)
{
ll l,r,ans=0;
for(l=1; l<=mx; l=r+1)
{
r=min(mx,x/(x/l));
ans=(ans+(l+r)%mod*(r-l+1)%mod*inv2%mod*(x/l)%mod)%mod;
}
return ans;
}
int main()
{
std::ios::sync_with_stdio(false);
exgcd(6,mod,inv6,y);
inv6=(inv6+mod)%mod;
exgcd(2,mod,inv2,y);
inv2=(inv2+mod)%mod;
ll n,m;
cin>>n>>m;
ll ans=(n%mod*n%mod-f(n,n)%mod+mod)%mod*(m%mod*m%mod-f(m,m)%mod+mod)%mod;
ll mn=min(n,m);
ans=(ans-m%mod*n%mod*mn%mod+mod+f(n,mn)%mod*m%mod+f(m,mn)%mod*n%mod)%mod;
ll l,r;
for(l=1; l<=mn; l=r+1)
{
r=min(m/(m/l),n/(n/l));
ans=(ans-(n/l)%mod*(m/l)%mod*(s(r)-s(l-1)%mod)%mod+mod)%mod;
}
cout<<ans<<endl;
return 0;
}