题意
有1~n镜子,每个镜子说你漂亮的概率是pi/100,如果第i个回答你漂亮那么就一直问到第n个说漂亮为止,否则重新从1开始问,一天只问一个镜子,问直到镜子n说你漂亮的期望天数。
思路
设Ei为问到第i个镜子直到第n个成功的期望天数。
看以下推导:
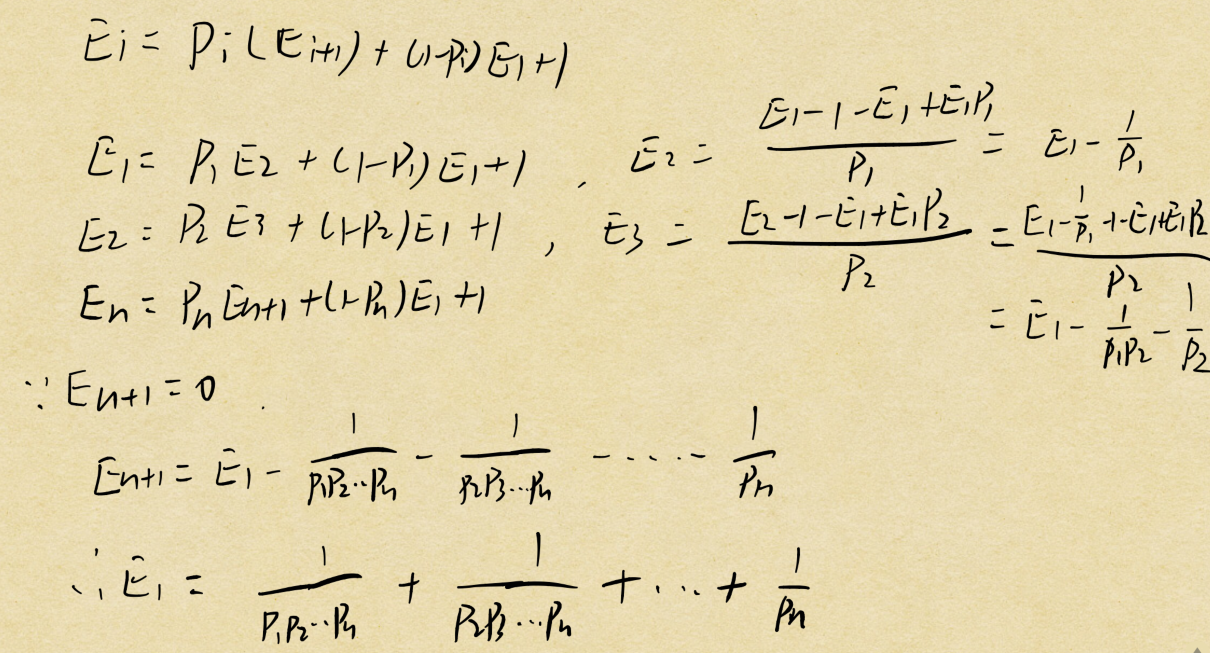
代码
#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
const int N=200005;
const int mod=998244353;
const double eps=1e-8;
const double PI = acos(-1.0);
#define lowbit(x) (x&(-x))
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qpow(ll a,ll b){ll res=1;while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}return res;}
ll inv(ll a,ll p){return qpow(a,p-2);}
ll read()
{
ll x=0;
char ch=getchar();
while(!isdigit(ch))
{
ch=getchar();
}
while(isdigit(ch))
{
x=x*10+(ch-'0');
ch=getchar();
}
return x;
}
ll p[N];
int main()
{
std::ios::sync_with_stdio(false);
ll n=read(),sum=0,tmp=1;
for(int i=1;i<=n;i++)
{
p[i]=read();
}
for(int i=n;i>=1;i--)
{
tmp=inv(p[i]*inv(100,mod)%mod,mod)*tmp%mod;
sum=(sum+tmp)%mod;
}
cout<<sum<<endl;
return 0;
}