CCF计算机职业资格认证考试题解系列文章为meelo原创,请务必以链接形式注明本文地址
CCF CSP 201312-3 最大的矩形
问题描述
在横轴上放了n个相邻的矩形,每个矩形的宽度是1,而第i(1 ≤ i ≤ n)个矩形的高度是hi。这n个矩形构成了一个直方图。例如,下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。
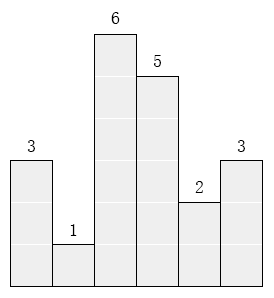
请找出能放在给定直方图里面积最大的矩形,它的边要与坐标轴平行。对于上面给出的例子,最大矩形如下图所示的阴影部分,面积是10。
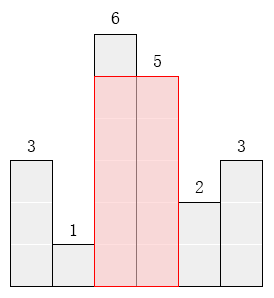
请找出能放在给定直方图里面积最大的矩形,它的边要与坐标轴平行。对于上面给出的例子,最大矩形如下图所示的阴影部分,面积是10。
输入格式
第一行包含一个整数n,即矩形的数量(1 ≤ n ≤ 1000)。
第二行包含n 个整数h1, h2, … , hn,相邻的数之间由空格分隔。(1 ≤ hi ≤ 10000)。hi是第i个矩形的高度。
第二行包含n 个整数h1, h2, … , hn,相邻的数之间由空格分隔。(1 ≤ hi ≤ 10000)。hi是第i个矩形的高度。
输出格式
输出一行,包含一个整数,即给定直方图内的最大矩形的面积。
样例输入
6
3 1 6 5 2 3
3 1 6 5 2 3
样例输出
10
解析
这里一道很经典的题目,许多网站上都有这道题目。题目很容易找到一个O(N2)的解,但是还存在一个更优的O(N)的解。
首先明确几个事实:最大矩形一定以N个矩阵之中的一个为高度。
因此问题可转换成以第i个矩阵为高度的最大面积。
代码
C++
#include "iostream" #include "stack" #include "vector" #include "algorithm" using namespace std; int getMaxArea(vector<int> &hist) { stack<int> s; int max_area = 0; int i = 0; int tp, area_with_top; while(i < hist.size()) { if(s.empty() || hist[s.top()] <= hist[i]) s.push(i++); else { tp = s.top(); s.pop(); area_with_top = hist[tp] * (s.empty() ? i : i-s.top()-1); max_area = max(max_area, area_with_top); } } while(!s.empty()) { tp = s.top(); s.pop(); area_with_top = hist[tp] * (s.empty() ? i : i-s.top()-1); max_area = max(max_area, area_with_top); } return max_area; } int main() { int N; vector<int> vec; cin >> N; for(int i=0; i<N; i++) { int val; cin >> val; vec.push_back(val); } cout << getMaxArea(vec); }