字符串的组合问题

题目：衔接上题，如果不是求字符的所有排列而是求所有字符的组合呢？还是输入三个字符a,b,c，则他们的组合有a,b,c,ab,ac,bc,abc.其中ab和ba只能算一个组合。

分析：组合问题也是可以用递归来解决的。首先，我们先来考虑这样一个问题，从M个不同字符中任取N个字符的所有组合，假设我们要求abc字符中任意两个字符的组合。也就是输入3个字符，求3个字符长度为2的组合。

我们可以这么想。从第一个字符开始(也就是a)，第一种情况，这个组合有a，那么剩下就2-1=1个字符和a组合了，要么是b，要么是c，分别组合成ab，ac。第二种情况，这个组合没有a，那么就剩下bc，由于规定的是2个字符的组合，也就只有bc了，这也是整个递归过程结束的条件。示意图如下：

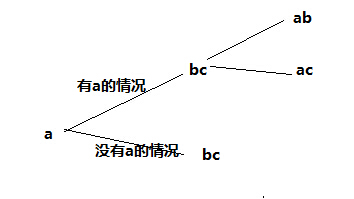
接下来我们再回归题目，要求的是所有字符的组合，也就是组合的长度是1,2,3...，思路其实是一样的，只是多了一个for循环，考虑组合长度1,2,3..多个情况。

void Combination(char *String)
{
    assert(String != NULL);
    int length = strlen(String);
    vector<char> result;
    //for循环对1,2,3...次的组合调用下面的Combination(String, i, result)打印出来
    for (int i = 1; i <= length; ++i)
        Combination(String, i, result);
}

void Combination(char *pString, int number, vector<char>& result)
{
    assert(pString != NULL);
    //1.递归出口
    if (*pString == '')
        return;
    //2.符合的条件情况，一一打印
    if (number == 0)
    {
        //计数
        static int num = 1;
        cout << num++ << " :  ";
        //终止的时候就打印结果
        vector<char>::iterator iter = result.begin();
        for (; iter != result.end(); ++iter)
            cout << *iter << "  ";
        cout << endl;
        return;                                         //别掉了，每次打印完了后，就进行下一次的打印
    }

    //3.进行递归成小问题
    result.push_back(*pString);                         //保存结果
    Combination(pString + 1, number - 1, result);       //当包含结点的时候
    result.pop_back();                                  //pop是因为下面不包含改结点的时候，指向的pString应该是一样的。                 
    Combination(pString + 1, number, result);           //当不包含该结点的时候
}

 扩展1---题目：输入两个整数n和m，从数列1,2,3...n中随意取几个数，使其和等于m，要求列出所有的组合。

分析：这其实就是一个组合问题，只是条件要求不一样罢了

#include "stdafx.h"
#include <iostream>
#include <vector>
using namespace std;
vector<int> result;
void find_factor(int sum, int n)
{
    //1.递归出口
    if (n <= 0 || sum <= 0)
        return;
    //2.输出找到的数
    if (sum == n)
    {
        for (vector<int>::iterator iter = result.begin(); iter != result.end(); ++iter)
            cout << *iter << "+";
        cout << n << endl;
    }
    //3.递归成小问题
    result.push_back(n);
    find_factor(sum - n, n - 1);  //n放在里面
    result.pop_back();
    find_factor(sum, n - 1);      //n不放在里面
}
int main(void)
{
    int sum, n;
    cin >> sum >> n;
    cout << "所有可能的序列，如下：" << endl;
    find_factor(sum, n);
    return 0;
}

总结一下：对于一些递归问题，首先要想到怎么做去符合递归条件，比如，终止的条件是什么？子问题的解应能组合成整个问题的解？子问题可通过再次递归调用求解？

一旦我们确定使用递归，那么整个算法包含这几个部分：1）.递归出口     2）满足条件（那么我们就输出这些结果） 3）递归成小问题。

参考：http://blog.sina.com.cn/s/blog_662234020101azp7.html

        http://blog.csdn.net/hackbuteer1/article/details/7462447