Open CV学习 01 离散傅里叶变换DFT

适用于图像处理的二维离散傅里叶变换

  

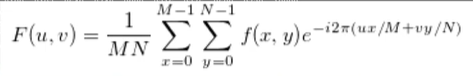
通常项目使用过程中由于DFT运算耗时，基本都会采用快速傅里叶变换。

 通过欧拉公式我们可以展开。

	cv::Mat mat(21, 7, CV_8UC1);
	cv::randu(mat, cv::Scalar::all(0), cv::Scalar::all(255));//为矩阵随机填充[0,255)的随机值
	std::cout << "original:
" << mat << std::endl << std::endl;

	cv::Mat paddedMat;
	int optimalRows = cv::getOptimalDFTSize(mat.rows);
	int optimalCols = cv::getOptimalDFTSize(mat.cols);
	
	//最优尺寸补零
	cv::copyMakeBorder(mat, paddedMat, 0, optimalRows - mat.rows, 0, optimalCols - mat.cols,cv::BORDER_CONSTANT, cv::Scalar::all(0));
    
	cv::Mat paddedMatDouble;
	paddedMat.convertTo(paddedMatDouble, CV_64FC1);
	
	Mat myresMat = mydft(paddedMatDouble);
	cv::Mat mydft_res_real_imaginary[] = { cv::Mat::zeros(myresMat.size(),CV_64FC1), Mat::zeros(myresMat.size(), CV_64FC1) };
	cv::split(myresMat, mydft_res_real_imaginary);//拆分数据

	Mat dftMat;
	cv::dft(paddedMatDouble, dftMat, DFT_COMPLEX_OUTPUT);
	cv::Mat dft_res_real_imaginary[] = { cv::Mat::zeros(dftMat.size(),CV_64FC1), Mat::zeros(dftMat.size(), CV_64FC1)};
	cv::split(dftMat, dft_res_real_imaginary);//拆分数据

	std::cout << "------------------------" << std::endl;
	for (int i = 0; i < dftMat.rows; i++)
	{
		double * myreal = mydft_res_real_imaginary[0].ptr<double>(i);
		double * myimg = mydft_res_real_imaginary[1].ptr<double>(i);
		double * real = dft_res_real_imaginary[0].ptr<double>(i);
		double * img = dft_res_real_imaginary[1].ptr<double>(i);
		for (int j = 0; j < dftMat.cols; j++)
		{
			std::cout << "-" << (std::abs(myreal[j] - real[j] - myimg[j] + img[j]) < 0.0001) << "- ";
		}
		std::cout << std::endl;
	}

Mat mydft(const Mat& mat)
{
	CV_Assert(mat.type() == CV_64FC1);
	int N = mat.cols;
	int M = mat.rows;
	Mat realMat(M, N, CV_64FC1);
	Mat imaginaryMat(M, N, CV_64FC1);

	for (int u = 0; u < M; u++)
	{
		double * ptrReal = realMat.ptr<double>(u);
		double * ptrImaginary = imaginaryMat.ptr<double>(u);
		for (int v = 0; v < N; v++)
		{
			double realSum = 0;
			double imaginary = 0;
			for (int x = 0; x < M; x++)
			{
				const double * ptrRow = mat.ptr<double>(x);
				for (int y = 0; y < N; y++)
				{
					realSum += ptrRow[y] * std::cos(-2. * CV_PI *(u * x * 1.0 / M + v * y * 1.0 / N));
					imaginary += ptrRow[y] * std::sin(-2. * CV_PI *(u * x * 1.0 / M + v * y * 1.0 / N));
				}

			}
			ptrReal[v] = realSum;
			ptrImaginary[v] = imaginary;
		}
	}

	Mat res;
	Mat planes[] = { realMat, imaginaryMat };
	merge(planes, 2, res);
	return res;
}

　　

 OpenCV提供的dft接口 void dft(InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0);

 dft函数的flags参数说明：

DFT_INVERSE  傅里叶逆变换

DFT_SCALE  与DFT_INVERSE结合使用，输出结果除以元素数来进行缩放

DFT_ROWS 对输入矩阵每一行进行傅里叶变换或逆变换，同时对多个向量进行变换，可以减少三围和多维变换操作的开销

DFT_COMPLEX_OUTPUT 傅里叶变换的结果是关于原点共轭对称的，两个原点对称点的值实部相等虚部相反，所以在一个象限中存储实部，对称象限存储虚部，这样，要两个通道存储的复数就只需要一个通道，节省内存。默认，如果输入为单通道，输出也为单通道（复共轭对称压缩存储复数); 如果输入为双通道，输出也为双通道复数结果；如果指定此参数，总是使用双通道输出结果。

DFT_REAL_OUTPUT 对共轭对称矩阵(如正向傅里叶变换生成的矩阵)进行反傅里叶变换时，结果是一个实数矩阵，但函数不会判断是否共轭对称，可以通过这个参数来告诉输入矩阵是共轭对称的，从而输出实数矩阵。如果输入只有一个通道(复共轭对称压缩存储复数),函数会认为这是一个经过压缩的共轭对称矩阵，从而输出实数矩阵。

DTF_COMPLEX_INPUT 输入必须要有两个通道分别表示实部和虚部，如果输入有两个通道，默认也认为是实部和虚部通道。