浅谈HashMap的内部实现

权衡时空

---

 

HashMap是以键值对的方式存储数据的。

如果没有内存限制，那我直接用哈希Map的键作为数组的索引，取的时候直接按索引get就行了，可是地价那么贵，哪里有无限制的地盘呢。

如果没有时间限制的话，我可以把数据放到一个无序数组中，按顺序查找，迟早也能找到。可是time is money，光阴那么短暂，谁又等得起呢。

所以，HashMap做了个折中的策略，使用适当的时间和空间做出了权衡，具体可以归结为“链表散列法”，这是一个hash表处理冲突的经典方法。

 　　

　　链表散列

---

那么什么是”链表散列法”呢？看下图：

 

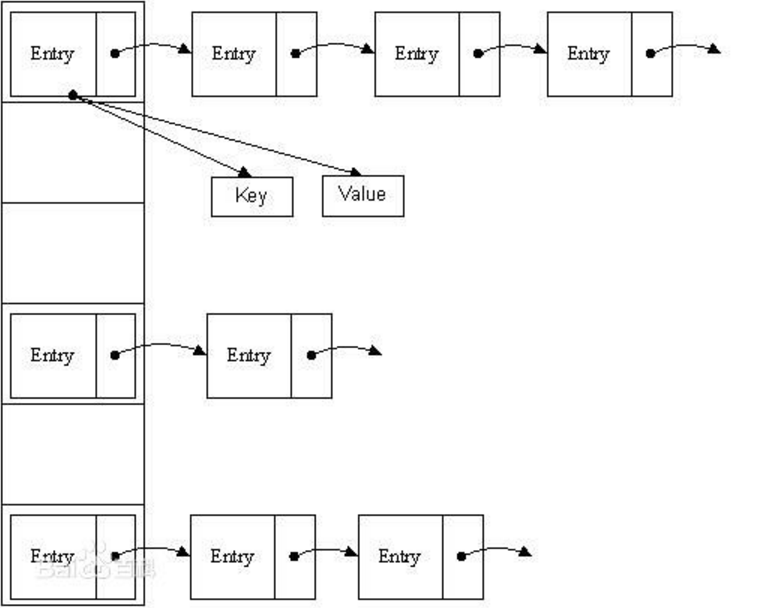
纵向的是一个数组，数组的每一项都是一个链表。你可以把这个数组看成是N个桶，每一个桶放着一个链子。

数组是干嘛的？数组的每一项负责放链表的。

链表是干嘛的？负责放Map数据的，比如一个HashMap有两个键，一个是key1，一个是key2。那么该链表就会分出两个节点分别存放这两个键值对（每一个键值对是打包放在Entry对象中的）。

链表是怎么链起来的？Entry包含有key、value、下一个节点next、hash值等，这个next就把各个节点串了起来。

HashMap保存数据的过程为：先计算当前要保存的键值对的哈希值（决定着当前键值对要放到哪个桶中），根据这个哈希值找到对应的桶。如果桶中没有数据，那就直接放进去。如果桶中已经放了数据（也即：桶中的链条上放着一个或者多个键值对），那就顺着桶中的这个链条一个一个比对，看有没有key与当前要保存的数据的key相同。如果有相同，直接覆盖原来key的value。如果没有相同的，那么将该元素保存在链头（最早保存的元素就会跑到链尾）。

 　　

　　装填因子

---

桶的数量决定了能放多少个HashMap，而具体用了多少个桶，则直接关系着查找的效率。打个比方，你去隔壁班找小明，班里有10个人，你很快就会找到小明，班里坐着100个人，你可能找半天才能找到。所以你去看HashMap的构造函数是这样的：

public HashMap(int initialCapacity, float loadFactor) {
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                                               initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                                               loadFactor);
        this.loadFactor = loadFactor;
        threshold = initialCapacity;
        init();
    }
public HashMap(int initialCapacity) {
        this(initialCapacity, DEFAULT_LOAD_FACTOR);
    }
public HashMap() {
        this(DEFAULT_INITIAL_CAPACITY, DEFAULT_LOAD_FACTOR);
}

三个构造函数都牵动着两个东西：initialCapacity，loadFactor。前者表示的是桶的初始数量（即数组大小），后者表示“装填因子”，装填因子是哈希表在其容量自动增加之前可以达到多满的一种尺度。比如，数组初始大小为100，如果装填因子=0.6，表示当数组中存放了60个Map之后，就要把数组扩容后才能继续存放。这就是为了解决上面讲到的效率问题。

装填因子定的小了，查找数据就快些，但是浪费空间。装填因子大了，空间利用率就高，但是浪费时间。生活就是这样，顾此失彼在所难免，万事哪有两全的呢。系统权衡利弊后，默认给的装填因子是0.75，这个一般我们是不需要改动的。

 　　

　　除留余数

---

那么还有个问题。拿到一个Map的哈希值，怎么决定放到哪个桶里呢？如果最后数组中的Map数据都挤到一块儿那可不行，查询就会慢。太松了也不行，浪费空间。Java用了一招“除留余数法”，保证数据在数组中分布均匀。

“除留余数法”，就是取模。比如数组的长度是100，Map的哈希值是80，用80%100，余数是80，就放到80那个位置。但是Java可不是那样干算的呦，且看源码：

void addEntry(int hash, K key, V value, int bucketIndex) {
        if ((size >= threshold) && (null != table[bucketIndex])) {
            resize(2 * table.length);
            hash = (null != key) ? hash(key) : 0;
            bucketIndex = indexFor(hash, table.length);
        }

        createEntry(hash, key, value, bucketIndex);
}

上面代码就是HashMap中的添加Entry数据的方法。BucketIndex就是当前Map在数组中的索引。第三行扩容且不谈，重点在indexFor方法，这个方法就是”取模”。我们点进去看一下：

static int indexFor(int h, int length) {

// assert Integer.bitCount(length) == 1 : "length must be a non-zero power of 2";

        return h & (length-1);

}

H是Map的哈希值，length是数组的长度。它直接使用了一个h & (length - 1)。这一句其实就相当于对数组取模，但是直接用二进制的位操作，比数学计算要快的多。这也给了我们程序员一个启发，能用位运算时尽量用，提高逼格又提高效率。

 　　

　　均匀分布

---

还有个有趣的地方，上面代码的注释部分：length must be a non-zero power of 2，这句是说，数组的长度必须是2的n次方。

为啥是2的n次方呢？

如果不是2的n次方，比如length为15，h分别为2,3,4。那么用h & (length -1)有：

h	Length-1	h & (length -1)
0010	1110	0010，即2
0011	1110	0010，即2
0100	1110	0100，即4

你看，随便测了三个数字，就发生了碰撞。为什么会这样呢？

这是因为：如果不是2的n次方，那么2^n – 1的最低位必然为0，而0、1分别和0作“与”运算，结果都为0。也就是说，不论h为多少，h & (length - 1)的结果最低位都是0。那么数组中最低位为1的那些位置就全部空缺着，这就导致数据在数组中分布不均匀了，继而影响了查询的效率。

读取数据的时候就简单多了，通过key的hash值找到在table数组中的索引处的Entry，然后返回该key对应的value即可。

参考资料：

http://www.cnblogs.com/chenssy/p/3521565.html

http://blog.csdn.net/zhuanshenweiliu/article/details/39177447

http://blog.csdn.net/tanggao1314/article/details/51457585#t1

http://www.importnew.com/18851.html