卑微的网课党来写博客了。。。
今天也是在家宅着的一天。
鸽巢原理(抽屉原理)
小例题 吃糖果
http://acm.hdu.edu.cn/showproblem.php?pid=1205
是一道典型的鸽巢原理题。可用隔板法进行分析。把拥有最多糖果数量n的一种糖果看成n个挡板,其余所有糖果数为s。
如果s<n-1,则将s个糖果放入挡板时,必定有两个挡板间没有糖果,也就是不能吃完糖,无解。
反之则有解。
#include<bits/stdc++.h> using namespace std; int a[1000002]; int main() { int t; scanf("%d",&t); while(t--) { int n,max=0,sum=0; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); if(max<a[i]) max=a[i]; } int i=1; for(i=1;i<=n;i++) { if(a[i]!=max) sum+=a[i]; if(sum>=max-1) break; } if(i==n+1) printf("No "); else printf("Yes "); } return 0; }
鸽巢定理加强形式
条件:鸽巢n个,鸽子m1+m2+...mn-n+1只,其中m1,m2,...,mn及n都是正整数。
结论:鸽巢1鸽子数>=m1, 或鸽巢2鸽子数>=m2,...或鸽巢n鸽子数>=mn,至少有一个成立。
Erdös-Szekeres定理
Ramsey定理
Ramsey定理:对于一个给定的两个整m,n>=2,则一定存在一个最小整数r,使得用两种颜色(例如红蓝)无论给Kr的每条边如何染色,总能找到一个红色的Km或者蓝色的Kn。
K表示完全图,即所有顶点间两两相连构成的图。
基本性质:
①等价性 r(m,n)=r(n,m)
②r(2,n)=n k2较特殊 只有一条边 最小的kr为Kn
③r(m,2)=m
部分Ramsey数表:

一些题目
Halloween treats
http://acm.hdu.edu.cn/showproblem.php?pid=1808
The first line of each test case contains two integers c and n (1 ≤ c ≤ n ≤ 100000), the number of children and the number of neighbours, respectively. The next line contains n space separated integers a1 , ... , an (1 ≤ ai ≤ 100000 ), where ai represents the number of sweets the children get if they visit neighbour i.
1 2 3 7 5
3 6
7 11 2 5 13 17
0 0
Sample Output
2 3 4
鸽巢原理的应用,大意是在n个数任取c个且是c的倍数的一种取法,输出取的元素的下标。
#include<bits/stdc++.h> long long c[100005],vis[100005],x; int main() { int m,n,i,j,flag,t; while(scanf("%d%d",&m,&n)&&n+m) { memset(vis,0,sizeof(vis)); for(c[0]=flag=0,i=1;i<=n;i++) { scanf("%I64d",&x); if(flag) continue; c[i]=c[i-1]+x; t=c[i]%m; if(t==0) { for(j=1;j<i;j++) printf("%d ",j); printf("%d ",j); flag=1; } else if(vis[t]) { for(j=vis[t]+1;j<i;j++) printf("%d ",j); printf("%d ",j); flag=1; } vis[t]=i; } } return 0; }
Friend-Graph
http://acm.hdu.edu.cn/showproblem.php?pid=6152
Problem Description
It is well known that small groups are not conducive of the development of a team. Therefore, there shouldn’t be any small groups in a good team.
In a team with n members,if there are three or more members are not friends with each other or there are three or more members who are friends with each other. The team meeting the above conditions can be called a bad team.Otherwise,the team is a good team.
A company is going to make an assessment of each team in this company. We have known the team with n members and all the friend relationship among these n individuals. Please judge whether it is a good team.
Input
The first line od each case should contain one integers n, representing the number of people of the team.(n<=3000)
Output
Sample Input
Sample Output
用Ramsey定理可以做。
#include<bits/stdc++.h> using namespace std; int a[10][10]; int main() { int T; scanf("%d",&T); while(T--) { int n; scanf("%d",&n); memset(a,0,sizeof(a)); for(int i=1;i<n;i++) { for(int j=i+1;j<=n;j++) { int t; scanf("%d",&t); if(t&&n<6) a[i][j]=a[j][i]=1; } } if(n>=6) { puts("Bad Team!"); continue; } int f=0; for(int i=1;i<=n;i++) { for(int j=i+1;j<=n;j++) { for(int k=j+1;k<=n;++k) { if(a[i][j]&&a[i][k]&&a[j][k]) { f=1; break; } } } } if(f) puts("Bad Team!"); else puts("Great Team!"); } return 0; }
排列与组合
排列
A(m,n)=m!/(m-n)!
组合
A(m,n)=C(m,n)*A(n,n)
C(m,n)=m!/((m-n)!*n!)
杨辉三角和二项式系数
杨辉三角大家应该都知道的,规律也很显然,每一个数由上一行对应的两个数之和。
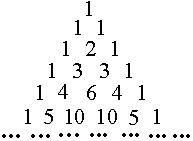
每一行展开的系数刚好对应杨辉三角每一行的数字。所以,杨辉三角可以用(1+x)n来定义和计算。
例题
杨辉三角
http://acm.hdu.edu.cn/showproblem.php?pid=2032
#include<bits/stdc++.h>
using namespace std; int a[31][31]; int main() { int i,j; for(i=1;i<=30;i++) { a[i][1]=1; for(j=2;j<=i;j++) { a[i][j]=a[i-1][j-1]+a[i-1][j]; } } int n; while(~scanf("%d",&n)) { for(i=1;i<=n;i++) { printf("%d",a[i][1]); for(j=2;j<=i;j++) printf(" %d",a[i][j]); printf(" "); } printf(" "); } return 0; }