计算几何

 

题目链接：https://acm.zcmu.edu.cn/JudgeOnline/problem.php?id=5073

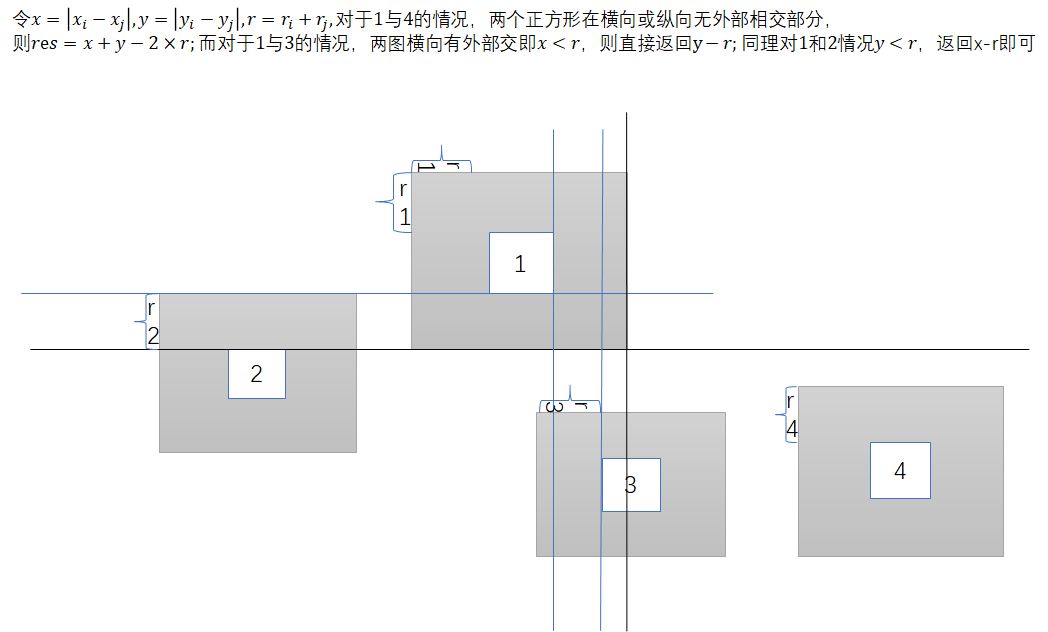
n个正方形，给出每个正方形中心及半径，m次修改（中心与半径）与查询（最近距离），由于给出的区域为x[0,10]，y[0,10]，直接暴力区间查询即可，注意若为0则直接跳出，否则会t，看别人思路是直接枚举正方形中的每一块分别求min|xi-xj|与min|yi-yj|，但经过画图可知共三种情况如下：

 

#include <map>
#include <vector>
#include <stdio.h>
#include <iostream>
#include <algorithm>
#define ll long long
#define ull unsigned ll
#define maxn 100005
#define maxm 600005
#define mod 998244353
using namespace std;
int t, n, m, len, ans;
int op, k, x, y, r;
int X[maxn], Y[maxn], R[maxn];

int solve(int i, int j){
    x = abs(X[i]-X[j]);
    y = abs(Y[i]-Y[j]);
    r = R[i]+R[j];
    if(x < r) //纵向外部重叠
        return y-r;
    else if(y < r) //横向外部重叠
        return x-r;
    int res = x+y-(r<<1); //无外部重叠
    return res;
}
int main(){
    scanf("%d", &t);
    while(t--){
        scanf("%d%d", &n, &m);
        for(int i = 1; i <= n; i ++){
            scanf("%d%d%d", X+i, Y+i, R+i);
        }
        int x, y, r;
        while(m--){
            scanf("%d", &op);
            if(op&1){
                scanf("%d%d%d%d", &k, &x, &y, &r);
                X[k] = x, Y[k] = y, R[k] = r;
            }else{
                int res = maxm;
                scanf("%d%d", &x, &y);
                for(int i = x; i < y; i ++){
                    for(int j = i+1; j <= y; j ++){
                        res = min(res, solve(i, j));
                        if(res <= 0)break;
                    }
                    if(res <= 0)break;
                }
                if(res <= 0)
                    printf("0
");
                else
                    printf("%d
", res);
            }
        }
    }
    return 0;
}

 

点到线段最短距离

//UVA10263
%:pragma GCC optimize("Ofast", 2)
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
#define Inf 0x7fffffff
#define maxn 1000005
int t, n, m, len, ans;
struct Point{
    double x, y;
    double dis(Point& a){ //距离
        return sqrt((x-a.x)*(x-a.x)+(y-a.y)*(y-a.y));
    }
    double dis2(Point& a){ //距离平方
        return (x-a.x)*(x-a.x)+(y-a.y)*(y-a.y);
    }
    double dotprd(Point& a, Point& b){ //点积
        return (x-a.x)*(b.x-a.x)+(y-a.y)*(b.y-a.y);
    }
    double crsprd(Point& a, Point& b){ //叉积
        return (x-a.x)*(b.y-a.y)-(b.x-a.x)*(y-a.y);
    }
}g[maxn];
double res;
Point r, p, temp;
void solve(Point a, Point b){
    double d = p.dotprd(a, b);
    if(d <= 0){ //向量间构成钝角
        d = p.dis(a);
        if(res > d){
            r = a;
            res = d;
        }
    }else if(d >= a.dis2(b)){ //向量间为锐角，但点与线段一端点构成向量在线段上投影比线段长
        d = p.dis(b);
        if(res > d){
            r = b;
            res = d;
        }
    }else{ //点投影在线段上
        double x = d/a.dis2(b); //线段与投影之比
        temp.x = a.x+x*(b.x-a.x);
        temp.y = a.y+x*(b.y-a.y);
        d = p.dis(temp);
        if(res > d){
            r = temp;
            res = d;
        }
    }
}
int main(){
    while(~scanf("%lf%lf%d", &p.x, &p.y, &n)){
        for(int i = 0; i < n+1; i ++){
            scanf("%lf%lf", &g[i].x, &g[i].y);
        }
        res = Inf;
        for(int i = 0; i < n; i ++){
            solve(g[i], g[i+1]);
        }
        printf("%.4lf
%.4lf
", r.x, r.y);
    }
    return 0;
}

 

三分

链接：https://ac.nowcoder.com/acm/contest/3006/B
来源：牛客网

由于牛牛战队经常要外出比赛，因此在全国各地建立了很多训练基地，每一个基地都有一个坐标(x,y)(x,y)。

这周末，牛牛队又要出去比赛了，各个比赛的赛点都在xx轴上。牛牛战队为了方便比赛，想找一个到达训练基地最大距离最小的地方作为比赛地。

 

#define EPS 1e-8
#define mod 1000000007
double PI = 3.14159265358;
const int N = 1005;
int t, n, m, len, ans;
double add(double a, double b){
    return (fabs(a + b) < EPS * (fabs(a) + fabs(b))) ? 0 : (a + b);
}
struct Point {
    double x, y;
    double dist(double a){
        return sqrt(add((x - a)*(x -a) ,(y)*(y) ));
    }
};
Point pt[maxn];
double f(double x){
    int i;
    double Max = 0;
    for( i = 0; i < n;  i++){
        Max = pt[i].dist(x) > Max ? pt[i].dist(x) : Max;
    }
    return Max;
}
double tri_search(){
    double Mid, Midmid, L,  R;
    L = -40000.0, R = 40000.0;
    while(L + EPS < R){
        Mid = (L + R) * 0.5;
        Midmid = (Mid + R) *0.5;
        if(f(Mid) <= f(Midmid ))
            R = Midmid;
        else L = Mid;
    }
    return L ;
}
int main(){
    while(~scanf("%d", &n) && n){
        for(int i =0 ; i < n; i++)
            scanf("%lf%lf" , &pt[i].x ,&pt[i].y );
        double xx = tri_search();
        double Max = f(xx);
        cout << Max << endl;
    }
    return 0;
}

 

平面内点构成的的钝角三角形个数

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 500 + 5;
typedef struct Point {
    ll x, y;
    Point() {}
    Point(ll x, ll y) : x(x), y(y) {}
    Point operator + (Point p) { return Point(x + p.x, y + p.y); }
    Point operator - (Point p) { return Point(x - p.x, y - p.y); }
    ll dot(Point p) { return x * p.x + y * p.y; } // 点积（钝角<0；直角==0；锐角>0）
    ll det(Point p) { return x * p.y - y * p.x; } // 叉积
    bool operator < (const Point& a) const {      // 极角升序
        if (y * a.y <= 0) {
            if (y > 0 || a.y > 0) return y > a.y;
            if (y == 0 && a.y == 0) return x > a.x;
        }
        return x * a.y - y * a.x > 0;
    }
}Vctor;
Point node[maxn];
Vctor vct[maxn * maxn];
int main(void)
{
    int n;    
    while (cin >> n) {
        for (int i = 0; i < n; ++i)
            cin >> node[i].x >> node[i].y;
        ll res = 0;
        for (int i = 0; i < n; ++i) {
            ll tot = 0;
            for (int j = 0; j < n; ++j) {
                if (i == j)        continue;
                vct[tot++] = node[j] - node[i];
            }
            sort(vct, vct + tot);
            for (int j = 0; j < tot; ++j)    vct[j + tot] = vct[j];    /* 3、4象限按照环类似的处理方式 */
            ll cnt1 = 0, cnt2 = 0;

            for (int j = 0; j < tot; ++j) {
                /*cnt在j左边*/            /* 3、4象限 */
                while (cnt1 <= j || (cnt1 < j + tot && vct[cnt1].det(vct[j]) < 0) && vct[j].dot(vct[cnt1]) >= 0/*锐角和直角*/) cnt1++;//左边锐角和直角个数（左边最大的非钝角）
                while (cnt2 <= j || (cnt1 < j + tot && vct[cnt2].det(vct[j]) < 0)) cnt2++;//左边所有角个数（左边最大的角）
                res += cnt2 - cnt1;
            }
        }
        cout << res << endl;
    }
    return 0;
}

 

最近点对

typedef struct{
    double x;
    double y;
}Point;
Point A, B;
vector<Point>vec;//存储点对
bool cmp_x(Point a, Point b){//x为第一关键字，y为第二关键字排序
    if(a.x == b.x)
        return a.y < b.y;
    return a.x < b.x;
}
bool cmp_y(Point a, Point b){//直接以y为关键字排序
    return a.y < b.y;
}
double dis(Point a, Point b){
    double x = a.x-b.x;
    double y = a.y-b.y;
    return x*x+y*y;
}
//寻找最近点对的点并返回最近距离
double compare(double d1, double d2, double d3, int l){
    /*三个点vec[l],vec[l+1],vec[l+2],两两比较之间l与l+2用2次，
    于是可以默认存储l与l+2点对，即d2对应的点对，然后与d1与d3比较时
    只需动A或B中的一个即可*/
    if(d1 < d2){
        d2 = d1;
        B = vec[l+1];
    }
    if(d3 < d2){
        d2 = d3;
        A = vec[l+1];
    }
    return d2;
}
double ClosestPoints(int l, int r){
    if(r-l == 1){
        A = vec[l], B = vec[l+1];
        return dis(vec[l], vec[l+1]);
    }else if(r-l == 2){
        A = vec[l], B = vec[l+2];//默认d2最小
        double d1 = dis(vec[l], vec[l+1]);
        double d2 = dis(vec[l], vec[l+2]);
        double d3 = dis(vec[l+1], vec[l+2]);
        return compare(d1, d2, d3, l);
    }else{
        int mid = (r+l)/2;
        //从mid为横坐标二分递归
        double min_left = ClosestPoints(l, mid);
        double min_right = ClosestPoints(mid+1, r);
        double d = min(min_left, min_right);
        vector<Point>res;
        for(int i = l; i <= r; i ++){
            if(fabs(vec[i].y-vec[mid].y) < d)
                res.push_back(vec[i]);
        }
        sort(res.begin(), res.end(), cmp_y);//以y为关键字从小到大排序
        for(int i = 0; i < (int)res.size()-1; i ++){//求取该区间内的最小点对
            for(int j = i+1; j < (int)res.size(); j ++){
                if(res[j].y-res[i].y >= d)
                    break;
                double dp = dis(res[i], res[j]);
                if(dp < d){
                    d = dp;
                    A = res[i];
                    B = res[j];
                }
            }
        }
        return d;
    }
}

int main(){
    int N; Point p;
    scanf("%d", &N);
    for(int i = 0; i < N; i ++){
        scanf("%lf%lf", &p.x, &p.y);
        vec.push_back(p);
    }
    sort(vec.begin(), vec.end(), cmp_x);
    ClosestPoints(0, vec.size()-1);
    printf("%.f %.f %.f %.f
", A.x, A.y, B.x, B.y);
}

 

凸包与直线交长

struct Point{
    double x, y;
    bool operator<(Point a)const{
        if(a.x == x)
            return a.y > y;
        return a.x > x;
    }
}g[maxn], p[maxn];
int t, m, n, k, len, flag;
Point a, b;
double dis(Point a, Point b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double multy(Point a, Point b, Point c){ //叉乘判线段位置关系
    return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}
Point getIntersect(Point a, Point b, Point c, Point d){ //求直线与边交点
    double per = ((a.x-c.x)*(c.y-d.y)-(c.x-d.x)*(a.y-c.y))/((a.x-b.x)*(c.y-d.y)-(c.x-d.x)*(a.y-b.y));
    a.x += (b.x-a.x)*per;
    a.y += (b.y-a.y)*per;
    return a;
}
bool isOnPoint(Point t, Point a, Point b){
    if(multy(t, a, b) == 0.0){
        if((t.x < a.x && t.x < b.x) || (t.x > a.x && t.x > b.x))
            return false;
        if((t.y < a.y && t.y < b.y) || (t.y > a.y && t.y > b.y))
            return false;
        return true;
    }
    return false;
}
bool isOnLine(Point a, Point b, Point c, Point d){ //线段互跨
    if(multy(a,c,b)*multy(a,d,b)<=0&&multy(c,a,d)*multy(c,b,d)<=0)
        return true;
    return false;
}
bool isIn(Point q){
    Point tmp = q;
    tmp.x = 1e15;
    Point t1, t2;
    int ans = 0;
    for(int i = 0; i < n; i ++){
        t1 = g[i], t2 = g[i+1];
        if(i == n-1)
            t2 = g[0];  //WA点
        if(isOnPoint(q, t1, t2)) //点在边上
            return 1;
        if(fabs(t1.y-t2.y) < EPS)
            continue;
        if(isOnPoint(t1, q, tmp)){ //直线经过点
            if(t1.y > t2.y)
                ans ++;
        }else if(isOnPoint(t2, q, tmp)){
            if(t2.y > t1.y)
                ans ++;
        }else if(isOnLine(q, tmp, t1, t2)){ //直线与边相交
            ans ++;
        }
    }
    return ans%2; //奇数在内，偶数在外
}
double solve(){
    Point t1, t2;
    int ans = 0, tot = 1;
    for(int i = 0; i < n; i ++){
        t1 = g[i], t2 = g[i+1];
        if(i == n-1)
            t2 = g[0];  //WA点
        if(fabs(multy(a, b, t1)) < EPS && fabs(multy(a, b, t2)) < EPS){ //直线与边重合
            p[ans++] = t1, p[ans++] = t2;
        }else if(multy(a, t1, b)*multy(a, t2, b) <= 0){ //相交
            p[ans++] = getIntersect(a, b, t1, t2);
        }
    }
    if(!ans)
        return 0.00;
    sort(p, p+ans);
    for(int i = 1; i < ans; i ++){ //去重
        t1 = p[i], t2 = p[i-1];
        if(fabs(t1.x-t2.x) < EPS && fabs(t1.y-t2.y) < EPS)
            continue;
        p[tot++] = p[i];
    }
    double sum = 0;
    for(int i = 1; i < tot; i ++){
        t1.x = (p[i].x+p[i-1].x)/2;
        t1.y = (p[i].y+p[i-1].y)/2;
        if(isIn(t1))
            sum += dis(p[i], p[i-1]);
    }
    return sum;
}
int main(){
    while(scanf("%d%d", &n, &m) && n+m){
        for(int i = 0; i < n; i ++){
            scanf("%lf%lf", &g[i].x, &g[i].y);
        }
        while(m--){
            scanf("%lf%lf%lf%lf", &a.x, &a.y, &b.x, &b.y);
            printf("%.3lf
", solve());
        }
    }
    return 0;
}

 

卷积模板（NTT）

//洛谷3803
int c, n, m, len, ans;
const ll mod = (119<<23)|1;
ll a[maxn>>1], b[maxn>>1], rev[maxn];
ll g = 3, gx = (mod+2)/3;
void init(){
    ans = 0, len = 1;
    fill(rev, rev+maxn, 0);
}
ll qpow(ll a, ll b){
    ll res = 1;
    while(b){
        if(b&1)
            res = res*a%mod;
        a = a*a%mod;
        b >>= 1;
    }
    return res%mod;
}
void NTT(ll *p, int c){
    ll x, y, pw;
    for(int i = 0; i < len; i ++){
        if(i < rev[i])
            swap(p[i], p[rev[i]]);
    }
    for(int i = 1; i < len; i <<= 1){
        pw = qpow(c+1?g:gx, (mod-1)/(i<<1));
        for(int j = 0; j < len; j += i<<1){
            ll q = 1;
            for(int k = 0; k < i; k ++, q = q*pw%mod){
                x = p[j+k], y = q*p[j+k+i]%mod;
                p[j+k] = (x+y)%mod, p[j+k+i] = (x-y+mod)%mod;
            }
        }
    }

}
int main(){
    while(~scanf("%d%d", &n, &m)){
        init();
        for(int i = 0; i <= n; i ++)
            scanf("%lld", &a[i]);
        for(int j = 0; j <= m; j ++)
            scanf("%lld", &b[j]);
        while(len <= m+n)
            len <<= 1, ans ++;
        for(int i = 0; i < len; i ++){
            rev[i] = (rev[i>>1]>>1|((i&1)<<(ans-1)));
        }
        NTT(a, 1), NTT(b, 1);
        for(int i = 0; i < len; i ++){
            a[i] = a[i]*b[i]%mod;
        }
        NTT(a, -1);
        ll inv = qpow(len, mod-2);
        for(int i = 0; i <= n+m; i ++){
            printf("%lld ", (a[i]*inv)%mod);
        }
        printf("
");
    }
    return 0;
}