生成符合高斯分布或者其他任意分布的随机数

在一些情况下经常需要用到随机数，而高斯随机数又是最常用到的。这一篇讲一下如何编程生成符合正态分布的高斯随机数，甚至任何其他分布的随机数。

我们知道C语言的标准库函数可以生成符合均匀分布的伪随机数。那么如何生成符合高斯分布的随机数呢？我们知道用逆函数法可以由符合(0,1)均匀分布的随机数得到符合任意分布的随机数，因此同样可以得到符合高斯分布的随机数。简单证明如下：

设随机变量u是符合(0,1)之间的均匀分布，那么有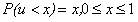。设随机变量X的累积分布函数（CDF）为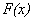，其逆函数为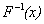。令随机变量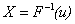。那么。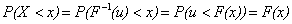

因此只要得到所需要的随机分布的累计分布函数（CDF）的逆函数，就可以简单的通过逆函数把(0,1)均匀分布的随机数变换成所需要的随机数。高斯分布的概率分布函数（PDF）为

，

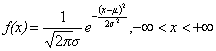其累计分布函数（CDF）是PDF的积分

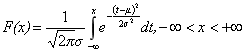，为从0到1的单调递增函数。

 

但是高斯分布的累积分布函数（CDF）不是初等函数，是没法用解析式表达的。再者符合高斯分布的随机变量的范围是从负无穷到正无穷的，是不可能用计算机生成的。即使用浮点数表示，也不是连续的。比如我们有(0,1)之间均匀分布的随机数，通过高斯分布CDF的逆函数变换到正负无穷，也只是得到一些离散的点。

因此要解决这些问题，首先用计算机生成的随机数肯定是离散的。比如C语言的rand()函数返回[0,RAND_MAX]之间的伪随机整数。所以我们也取一定范围的整数作为生成的随机高斯数。然后根据高斯分布的性质，离均值越远，概率越小，通常3σ以外的地方可以近似的认为概率为0。所以可以截断高斯分布的范围，让生成的高斯随机数位于[μ-3σ,μ+3σ]。这样CDF的无穷积分就可以由有限的求和运算代替了。算法描述如下：

1. 设定高斯随机数的范围是[0,2r]，则均值是r，σ=r/3。
2. 由PDF计算截断的概率分布，然后求和计算累积分布。
3. 输入一个均匀分布的随机数。从小到大搜索高斯累积分布，第一个大于均匀分布随机数的的累积分布即为对应的高斯随机数。重复3，即可产生符合同样高斯分布的一系列随机数 。
4. 如果所需高斯随机数的范围有变化，需从第一步重新开始。

再看一下如何生成均匀分布的随机数。最方便就是用C语言的rand()函数。在很多系统上RAND_MAX是32767，有时候范围不太够用，这样很不方便。这里我用如下代码生成。

unsigned long _RandomNumber = time(NULL);
#define GET_NEXT_RANDOM (_RandomNumber = (_RandomNumber << 7) + (_RandomNumber >> 7))

 只要初始数不为0，就可以连续生成一系列的伪随机数。经过实验，我觉得可以满足一般使用。而优点就是，随机数的范围就是你设定的随机数的类型所能取得的范围。相对于rand()来说，运算速度更快。

 生成高斯随机数的C代码如下，GaussianRandom()返回一个在[0,2r]的高斯随机数。为了避免浮点数的比较，计算PDF和CDF都乘以一个大常数转为整数。

static unsigned int *pGaussianCD = NULL;

void GaussCDF(int radius)
{
    unsigned int Weight;
    int j, n = 0;

    n = 2*radius + 1;
    if ((pGaussianCD = realloc(pGaussianCD, sizeof(unsigned int) * n)) == NULL)
    {
        printf("memory failure!
");
        exit(-1);
    }

    float sigma = radius / 3.0f;
    float sigma22 = 2*sigma*sigma;
    float sigma_sqrt2PI = sqrtf(2*PI)*sigma;
    Weight = (unsigned int)(expf(-(radius*radius)/sigma22) / sigma_sqrt2PI * 65536.0f);
    *pGaussianCD = Weight;
    n = 1;
    for (j = -radius + 1; j <= radius; j++)
    {
        Weight = (unsigned int)(expf(-(j*j)/sigma22) / sigma_sqrt2PI * 65536.0f);
        pGaussianCD[n] = Weight + pGaussianCD[n-1];
        n++;
    }
}

/* Return a Gaussian random number between [0, 2*r], mean is r. */
unsigned int GaussianRandom(int radius)
{
    static int r = 0, mn, m;
    int rand, i;

    if (r != radius)
    {
        r = radius;
        /* recalculate CDF */
        GaussCDF(r);
        mn = 2*r;
        m = pGaussianCD[mn] + 1;
    }
    rand = GET_NEXT_RANDOM % m;
    
    for (i = 0; i <= mn; i++)
    {
        if (rand <= pGaussianCD[i])
            return i;
    }
    /* should not reach here */ 
    assert(0);
    return r; 
}

产生一个高斯随机数主要时间都花在搜索输入的均匀随机数在高斯累计分布上的位置。产生高斯随机数的范围越大，相对花的时间越长。但是我们知道高斯分布的均值附近是产生随机数概率最高的地方。如果从均值开始向两侧搜索，则有可能最快搜索到，就大大缩短了花费的时间。把最后一个搜索循环修改如下即可。

    if (rand <= pGaussianCD[radius])
    {
        i = radius - 1;
        while (i >= 0)
        {
            if (rand > pGaussianCD[i])
                return i + 1;
            i--;
        }
        return 0;
    }
    else
    {
        i = radius + 1;
        while (i <= mn)
        {
            if (rand <= pGaussianCD[i])
                return i;
            i++;
        }
    }

我们来看一下产生的高斯随机数的分布如何，同时看看用移位加产生伪随机数的方法是否可行。下面左边的图是用移位加的方法生成的[0,200]之间的24万个伪随机数和24万个高斯随机数的分布。作为对比右边的图是用rand()生成的，看起来没什么大的差别。

 

            移位加生成随机数分布                          rand()生成随机数分布

 

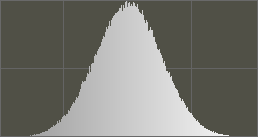
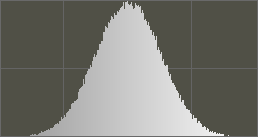
         移位加生成高斯随机数分布                     rand()生成高斯随机数分布

这样，我们就可以生成任意分布的随机数，即使它的CDF不能用初等函数表达。下图是生成24万个泊松随机数的分布，λ=7。因为离开λ的地方的概率下降很快，横轴拉大了便于观察。

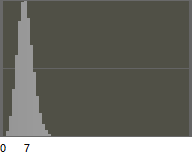
      生成泊松随机数分布