OpenCV学习(18) 细化算法(6)

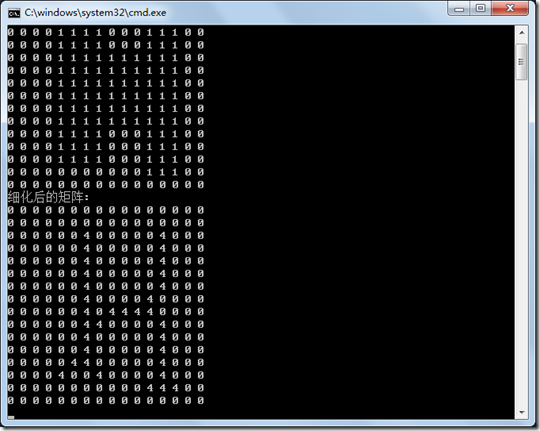
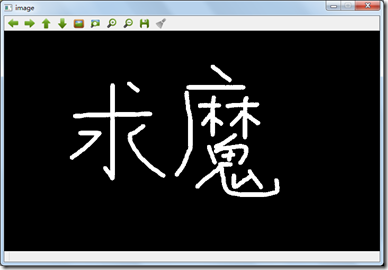
本章我们在学习一下基于索引表的细化算法。

假设要处理的图像为二值图，前景值为1，背景值为0。

索引表细化算法使用下面的8邻域表示法：

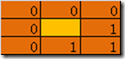
一个像素的8邻域，我们可以用8位二进制表示，比如下面的8邻域，表示为00111000=0x38=56

我们可以枚举出各种情况下，当前像素能否删除的表，该表大小为256。它的索引即为8邻域表示的值，表中存的值为0或1，0表示当前像素不能删除，1表示可以删除。deletemark[256]

比如下图第一个表示，索引值为0，它表示孤立点，不能删除，所以deletemark[0]=0,第二个表示索引值为17，它表示端点，也不能删除，所以deletemark[17]=0，第三个表示索引为21，删除的话会改变连通域数量，所以deletemark[21]=0，第四个表示索引值为96，此时可以删除，所以deletemark[96]=1。

最终我们会定义一张完整的表来表示当前像素能否删除。

索引表细化算法描述很简单。

1.找到轮廓，其值用4表示

2.查找值为4的轮廓，查找索引表判断能否删除，能删除的话把它置为0。

循环迭代1，2直到再也没有可以删除的点为止。

下面的算法的代码：

void gThin::cvidxThin1(cv::Mat& src, cv::Mat& dst)
        {


        if(src.type()!=CV_8UC1)
            {
            printf("只能处理二值或灰度图像
");
            return;
            }
        //非原地操作时候，copy src到dst
        if(dst.data!=src.data)
            {
            src.copyTo(dst);
            }

        //    P0 P1 P2
        //    P7    P3
        //    P6 P5 P4
        unsigned char deletemark[256] = {
            0,0,0,0,0,0,0,1,    0,0,1,1,0,0,1,1,
            0,0,0,0,0,0,0,0,    0,0,1,1,1,0,1,1,
            0,0,0,0,0,0,0,0,    1,0,0,0,1,0,1,1,
            0,0,0,0,0,0,0,0,    1,0,1,1,1,0,1,1,
            0,0,0,0,0,0,0,0,    0,0,0,0,0,0,0,0,
            0,0,0,0,0,0,0,0,    0,0,0,0,0,0,0,0,
            0,0,0,0,0,0,0,0,    1,0,0,0,1,0,1,1,
            1,0,0,0,0,0,0,0,    1,0,1,1,1,0,1,1,
            0,0,1,1,0,0,1,1,    0,0,0,1,0,0,1,1,
            0,0,0,0,0,0,0,0,    0,0,0,1,0,0,1,1,
            1,1,0,1,0,0,0,1,    0,0,0,0,0,0,0,0,
            1,1,0,1,0,0,0,1,    1,1,0,0,1,0,0,0,
            0,1,1,1,0,0,1,1,    0,0,0,1,0,0,1,1,
            0,0,0,0,0,0,0,0,    0,0,0,0,0,1,1,1,
            1,1,1,1,0,0,1,1,    1,1,0,0,1,1,0,0,
            1,1,1,1,0,0,1,1,    1,1,0,0,1,1,0,0
            };//索引
        int i, j;
        int width, height;
        //之所以减1，是方便处理8邻域，防止越界
        width = src.cols -1;
        height = src.rows -1;
        int step = src.step;
        int  p0, p1, p2,p3,p4,p5,p6,p7;
        uchar* img;
        bool ifEnd;
        bool border = false; //交换删除的次序，防止从一边细化
        while(1)
            {

            border = !border;
            img = dst.data;
            for(i = 1; i < height; i++)
                {
                img += step;
                for(j =1; j<width; j++)
                    {
                    uchar* p = img + j;
                    //如果p点是背景点,继续循环
                    if(p[0]==0) continue;
                    p0 = p[-step-1]>0?1:0;
                    p1 = p[-step]>0?1:0;
                    p2 = p[-step+1]>0?1:0;
                    p3 = p[1]>0?1:0;
                    p4 = p[step+1]>0?1:0;
                    p5 = p[step]>0?1:0;
                    p6 = p[step-1]>0?1:0;
                    p7 = p[-1]>0?1:0;

                    //如果sum等于0，则不是内部点，是轮廓点，设置其像素值为2
                    int sum;
                    sum =  p0 & p1 & p2 & p3 & p4 & p5 & p6 & p7;

                    //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
                    if(sum==0)
                        {
                        dst.at<uchar>(i,j) = 4; //满足删除条件，设置当前像素为0
                        }

                    }
                }
            //printf("
");
            //PrintMat(dst);
            //执行删除操作
            ifEnd = false;

            img = dst.data;
            for(i = 1; i < height; i++)
                {
                img += step;
                for(j =1; j<width; j++)
                    {
                    uchar* p = img + j;
                    //如果p点是背景点,继续循环
                    if(p[0]!=4) continue;
                    p0 = p[-step-1]>0?1:0;
                    p1 = p[-step]>0?1:0;
                    p2 = p[-step+1]>0?1:0;
                    p3 = p[1]>0?1:0;
                    p4 = p[step+1]>0?1:0;
                    p5 = p[step]>0?1:0;
                    p6 = p[step-1]>0?1:0;
                    p7 = p[-1]>0?1:0;

                    p1 = p1<<1;
                    p2 = p2<<2;
                    p3 = p3 <<3;
                    p4 = p4<<4;
                    p5 = p5<<5;
                    p6 = p6 <<6;
                    p7 = p7 << 7;

                    //求的8邻域在索引表中的索引
                    int sum;
                    sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7;

                    //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
                    if(deletemark[sum] == 1)
                        {
                        dst.at<uchar>(i,j) = 0; //满足删除条件，设置当前像素为0
                        ifEnd = true;
                        }

                    }
                }
            
            //printf("
");
            //PrintMat(dst);
            //printf("
");

            //已经没有可以细化的像素了，则退出迭代
            if(!ifEnd) break;
            }

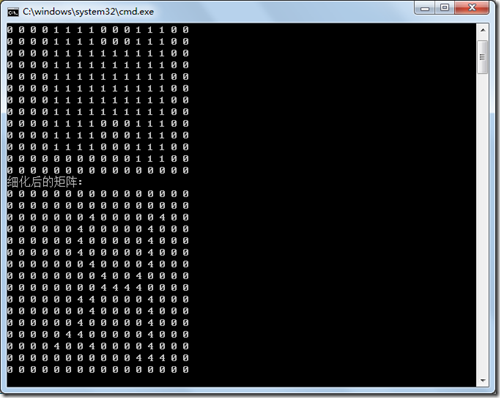
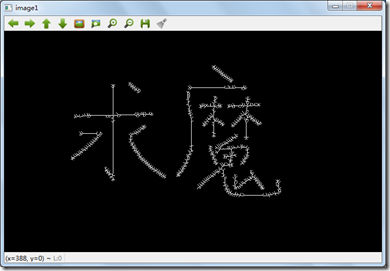
上面的算法可以看到细化后的轮廓偏右了，我们可以更改删除的循环条件，把循环拆分成三个，修改后的代码如下：

void gThin::cvidxThin(cv::Mat& src, cv::Mat& dst)
    {


    if(src.type()!=CV_8UC1)
        {
        printf("只能处理二值或灰度图像
");
        return;
        }
    //非原地操作时候，copy src到dst
    if(dst.data!=src.data)
        {
        src.copyTo(dst);
        }

    //    P0 P1 P2
    //    P7    P3
    //    P6 P5 P4
    unsigned char deletemark[256] = {
        0,0,0,0,0,0,0,1,    0,0,1,1,0,0,1,1,
        0,0,0,0,0,0,0,0,    0,0,1,1,1,0,1,1,
        0,0,0,0,0,0,0,0,    1,0,0,0,1,0,1,1,
        0,0,0,0,0,0,0,0,    1,0,1,1,1,0,1,1,
        0,0,0,0,0,0,0,0,    0,0,0,0,0,0,0,0,
        0,0,0,0,0,0,0,0,    0,0,0,0,0,0,0,0,
        0,0,0,0,0,0,0,0,    1,0,0,0,1,0,1,1,
        1,0,0,0,0,0,0,0,    1,0,1,1,1,0,1,1,
        0,0,1,1,0,0,1,1,    0,0,0,1,0,0,1,1,
        0,0,0,0,0,0,0,0,    0,0,0,1,0,0,1,1,
        1,1,0,1,0,0,0,1,    0,0,0,0,0,0,0,0,
        1,1,0,1,0,0,0,1,    1,1,0,0,1,0,0,0,
        0,1,1,1,0,0,1,1,    0,0,0,1,0,0,1,1,
        0,0,0,0,0,0,0,0,    0,0,0,0,0,1,1,1,
        1,1,1,1,0,0,1,1,    1,1,0,0,1,1,0,0,
        1,1,1,1,0,0,1,1,    1,1,0,0,1,1,0,0
        };//索引
    int i, j;
    int width, height;
    //之所以减1，是方便处理8邻域，防止越界
    width = src.cols -1;
    height = src.rows -1;
    int step = src.step;
    int  p0, p1, p2,p3,p4,p5,p6,p7;
    uchar* img;
    bool ifEnd;
    bool border = false; //交换删除的次序，防止从一边细化
    while(1)
        {

        border = !border;
        img = dst.data;
        for(i = 1; i < height; i++)
            {
            img += step;
            for(j =1; j<width; j++)
                {
                uchar* p = img + j;
                //如果p点是背景点,继续循环
                if(p[0]==0) continue;
                p0 = p[-step-1]>0?1:0;
                p1 = p[-step]>0?1:0;
                p2 = p[-step+1]>0?1:0;
                p3 = p[1]>0?1:0;
                p4 = p[step+1]>0?1:0;
                p5 = p[step]>0?1:0;
                p6 = p[step-1]>0?1:0;
                p7 = p[-1]>0?1:0;

                //如果sum等于0，则不是内部点，是轮廓点，设置其像素值为2
                int sum;
                sum =  p0 & p1 & p2 & p3 & p4 & p5 & p6 & p7;

                //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
                if(sum==0)
                    {
                    dst.at<uchar>(i,j) = 4; //满足删除条件，设置当前像素为0
                    }

                }
            }
        //printf("
");
        //PrintMat(dst);
        //执行删除操作
        ifEnd = false;

        img = dst.data;
        for(i = 1; i < height; i++)
            {
            img += step;
            for(j =1; j<width; j+=3)
                {
                uchar* p = img + j;
                //如果p点是背景点,继续循环
                if(p[0]!=4) continue;
                p0 = p[-step-1]>0?1:0;
                p1 = p[-step]>0?1:0;
                p2 = p[-step+1]>0?1:0;
                p3 = p[1]>0?1:0;
                p4 = p[step+1]>0?1:0;
                p5 = p[step]>0?1:0;
                p6 = p[step-1]>0?1:0;
                p7 = p[-1]>0?1:0;

                p1 = p1<<1;
                p2 = p2<<2;
                p3 = p3 <<3;
                p4 = p4<<4;
                p5 = p5<<5;
                p6 = p6 <<6;
                p7 = p7 << 7;

                //求的8邻域在索引表中的索引
                int sum;
                sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7;

                //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
                if(deletemark[sum] == 1)
                    {
                    dst.at<uchar>(i,j) = 0; //满足删除条件，设置当前像素为0
                    ifEnd = true;
                    }

                }
            }

        img = dst.data;
        for(i = 1; i < height; i++)
            {
            img += step;
            for(j =2; j<width; j+=3)
                {
                uchar* p = img + j;
                //如果p点是背景点,继续循环
                if(p[0]!=4) continue;
                p0 = p[-step-1]>0?1:0;
                p1 = p[-step]>0?1:0;
                p2 = p[-step+1]>0?1:0;
                p3 = p[1]>0?1:0;
                p4 = p[step+1]>0?1:0;
                p5 = p[step]>0?1:0;
                p6 = p[step-1]>0?1:0;
                p7 = p[-1]>0?1:0;

                p1 = p1<<1;
                p2 = p2<<2;
                p3 = p3 <<3;
                p4 = p4<<4;
                p5 = p5<<5;
                p6 = p6 <<6;
                p7 = p7 << 7;

                //求的8邻域在索引表中的索引
                int sum;
                sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7;

                //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
                if(deletemark[sum] == 1)
                    {
                    dst.at<uchar>(i,j) = 0; //满足删除条件，设置当前像素为0
                    ifEnd = true;
                    }

                }
            }

        img = dst.data;
        for(i = 1; i < height; i++)
            {
            img += step;
            for(j =3; j<width; j+=3)
                {
                uchar* p = img + j;
                //如果p点是背景点,继续循环
                if(p[0]!=4) continue;
                p0 = p[-step-1]>0?1:0;
                p1 = p[-step]>0?1:0;
                p2 = p[-step+1]>0?1:0;
                p3 = p[1]>0?1:0;
                p4 = p[step+1]>0?1:0;
                p5 = p[step]>0?1:0;
                p6 = p[step-1]>0?1:0;
                p7 = p[-1]>0?1:0;

                p1 = p1<<1;
                p2 = p2<<2;
                p3 = p3 <<3;
                p4 = p4<<4;
                p5 = p5<<5;
                p6 = p6 <<6;
                p7 = p7 << 7;

                //求的8邻域在索引表中的索引
                int sum;
                sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7;

                //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
                if(deletemark[sum] == 1)
                    {
                    dst.at<uchar>(i,j) = 0; //满足删除条件，设置当前像素为0
                    ifEnd = true;
                    }

                }
            }

        //printf("
");
        //PrintMat(dst);
        //printf("
");

        //已经没有可以细化的像素了，则退出迭代
        if(!ifEnd) break;
        }

    }

修改后的结果：

程序源代码：工程FirstOpenCV11