网络流好题!!!
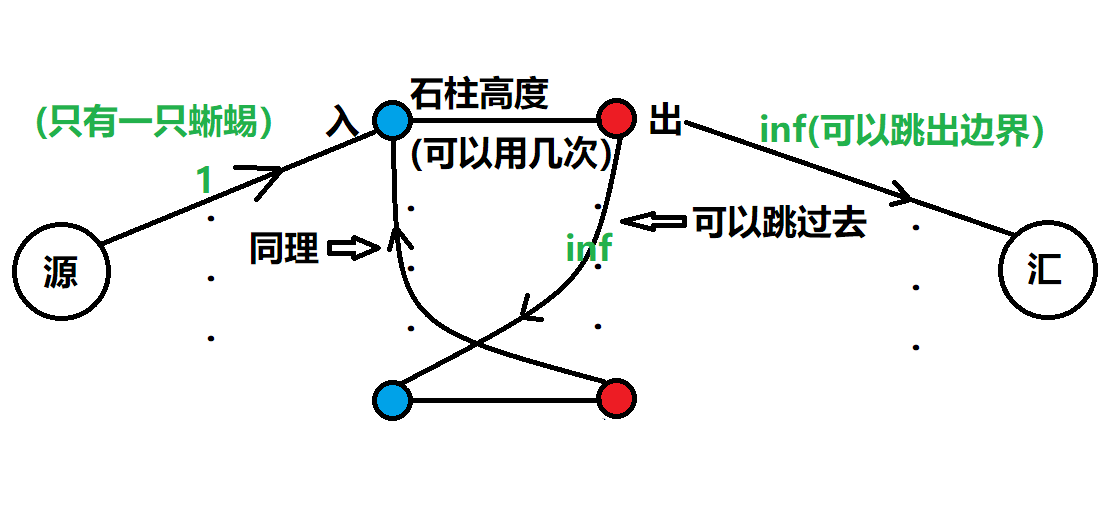
网络流一般都难在建图,后来看到题解里没有一张用来解释的图我就太发一张。
这道题难在把石柱拆点(入口,出口),把石柱高度想成可以用多少次。
我们首先从源点向各个石柱的入口连边(有蜥蜴)边长为1
接着,我们把各个石柱的入口与出口连边(边长为石柱高度)
下一步,我们把各个距离不超过d的石柱连边:出口---入口
最后,我们把各个石柱与汇点连边(可以跳出边界)
上图:
上代码:
1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 #define ll long long 7 #define max(x,y) ((x)>(y)?(x):(y)) 8 #define min(x,y) ((x)<(y)?(x):(y)) 9 #define fur(i,x,y) for(i=x;i<=y;i++) 10 #define fdr(i,x,y) for(i=x;i>=y;i--) 11 #define Fur(i,x,y) for(ll i=x;i<=y;i++) 12 #define Fdr(x,y) for(ll i=x;i>=y;i--) 13 #define in2(x,y) in(x);in(y) 14 #define in3(x,y,z) in2(x,y);in(z) 15 #define in4(a,b,c,d) in2(a,b);in2(c,d) 16 #define clr(x,y) memset(x,y,sizeof(x)) 17 #define cpy(x,y) memcpy(x,y,sizeof(x)) 18 #define fl(i,x) for(ll i=head[x],to;to=e[i].to,i;i=e[i].next) 19 #define inf 233333333 20 using namespace std; 21 /*---------------------------------------*/ 22 namespace fib{char b[300000]= {},*f=b;} 23 #define gc ((*fib::f)?(*(fib ::f++)):(fgets(fib::b,sizeof(fib::b),stdin)?(fib::f=fib::b,*(fib::f++)):-1)) 24 inline void in(ll &x){x=0;char c;bool f=0;while((c=gc)>'9'||c<'0')if(c=='-')f=!f;x=c-48;while((c=gc)<='9'&&c>='0')x=x*10+c-48;if(f)x=-x;} 25 namespace fob{char b[300000]= {},*f=b,*g=b+300000-2;} 26 #define pob (fwrite(fob::b,sizeof(char),fob::f-fob::b,stdout),fob::f=fob::b,0) 27 #define pc(x) (*(fob::f++)=(x),(fob::f==fob::g)?pob:0) 28 struct foce{~foce(){pob;fflush(stdout);}} _foce; 29 namespace ib{char b[100];} 30 inline void out(ll x){if(x==0){pc(48);return;}if(x<0){pc('-');x=-x;}char *s=ib::b;while(x) *(++s)=x%10,x/=10;while(s!=ib::b) pc((*(s--))+48);} 31 inline void outn(ll x){out(x);pc(' ');} 32 inline void swap(ll &x,ll &y){ll t=x;x=y;y=t;} 33 inline ll jdz(ll x){return x>=0?x:-x;} 34 /*------------------------------------------------------------------------------------------------*/ 35 36 /*------------------------------------------------------------------------------------------------*/ 37 #define N 5001 38 struct edge{ll w,to,next;}e[N*N/4]; 39 ll head[N],n,m,r,c,k,st,ed,cnt=2,q[N],d[N],b=0,ps=1,ans=0; 40 bool v[21][21]; 41 inline void add(ll x,ll y,ll w){ 42 e[cnt].w=w;e[cnt].to=y;e[cnt].next=head[x];head[x]=cnt++; 43 swap(x,y);e[cnt].w=0;e[cnt].to=y;e[cnt].next=head[x];head[x]=cnt++; 44 } 45 inline bool bfs(){ 46 ll h=0,t=1,x;clr(d,0); 47 q[h]=st;d[st]=1; 48 while(h<t){ 49 x=q[h++];if(x==ed)return 1; 50 fl(i,x)if(e[i].w&&!d[to]){d[to]=d[x]+1;q[t++]=to;} 51 }return 0; 52 } 53 inline ll dfs(ll x,ll mf){ 54 if(x==ed)return mf; 55 ll u=0,w; 56 fl(i,x) 57 if(e[i].w&&d[to]==d[x]+1){ 58 w=mf-u; 59 w=dfs(to,min(w,e[i].w)); 60 e[i].w-=w;e[i^1].w+=w; 61 u+=w; 62 if(u==mf)return u; 63 } 64 if(!u)d[x]=-1; 65 return u; 66 } 67 inline bool pd(ll x,ll y){return x*x+y*y<=k*k;} 68 struct sz{ll l,r,x,y;}p[N]; 69 int main(){ 70 in3(r,c,k);ed=1; 71 char s[21]; 72 Fur(i,1,r){ 73 scanf("%s",s+1); 74 Fur(j,1,c) 75 if(s[j]!=48){ 76 p[++b].l=++ps;p[b].r=++ps;add(ps-1,ps,s[j]-48); 77 p[b].x=i;p[b].y=j; 78 if(i<=k||j<=k||r-i+1<=k||c-j+1<=k)add(ps,ed,inf); 79 } 80 } 81 Fur(i,1,b)Fur(j,i+1,b) 82 if(pd(p[i].x-p[j].x,p[i].y-p[j].y))add(p[i].r,p[j].l,inf),add(p[j].r,p[i].l,inf); 83 Fur(i,1,r){scanf("%s",s+1);Fur(j,1,c)if(s[j]=='L')ans--,v[i][j]=1;}st=ps+1; 84 Fur(i,1,b)if(v[p[i].x][p[i].y])add(st,p[i].l,1); 85 86 while(bfs())ans+=dfs(st,inf); 87 out(-ans); 88 } 89 90 /* 91 92 */