逻辑回归属于有监督学习,就是说每个样本点都是有标签的。逻辑回归用来做二分类,也就是说输出只有2个类别。
一、逻辑回归的模型
当前有m个样本点,其中第 i 个样本点记作 ((x^{(i)}, y^{(i)}))。特征维度为n,即 $x^{(i)} $是n维列向量, (x^{(i)} = [x_1^{(i)}, x_2^{(i)},cdots, x_n^{(i)}]^T)。(y^{(i)})等于0或1。
逻辑回归的参数为系数向量 ( heta = [ heta_1, heta_2, cdots, heta_n]^T)。
在线性回归中,使用x和( heta)的内积,作为(y^{(i)})的预测值,用矩阵形式这么写:
[ heta^T x^{(i)} =
left[
egin{matrix}
heta_1 & heta_2 & cdots & heta_n
end{matrix}
ight]
left[
egin{matrix}
x_1^{(i)} \
x_2^{(i)} \
vdots \
x_n^{(i)}
end{matrix}
ight]
= heta_1 x_1^{(i)} + heta_2 x_2^{(i)} + cdots + heta_n x_n^{(i)}
]
利用 $ heta^T x^{(i)} $将输入变量映射到了 (-infty)到(+infty),但是我们要做的是二分类问题,输出应该为离散值。 刚好在数学中有sigmoid函数:
[g(z) = frac{1}{1+e^{-z}}
]
sigmoid函数图像如下,比较像阶跃函数的的一个平滑,可以把取值为R的自变量映射到(0, 1)。利用sigmoid函数可以大概做分类:如果自变量大于0,就认为类别为1;如果自变量小于0,就认为类别为0。
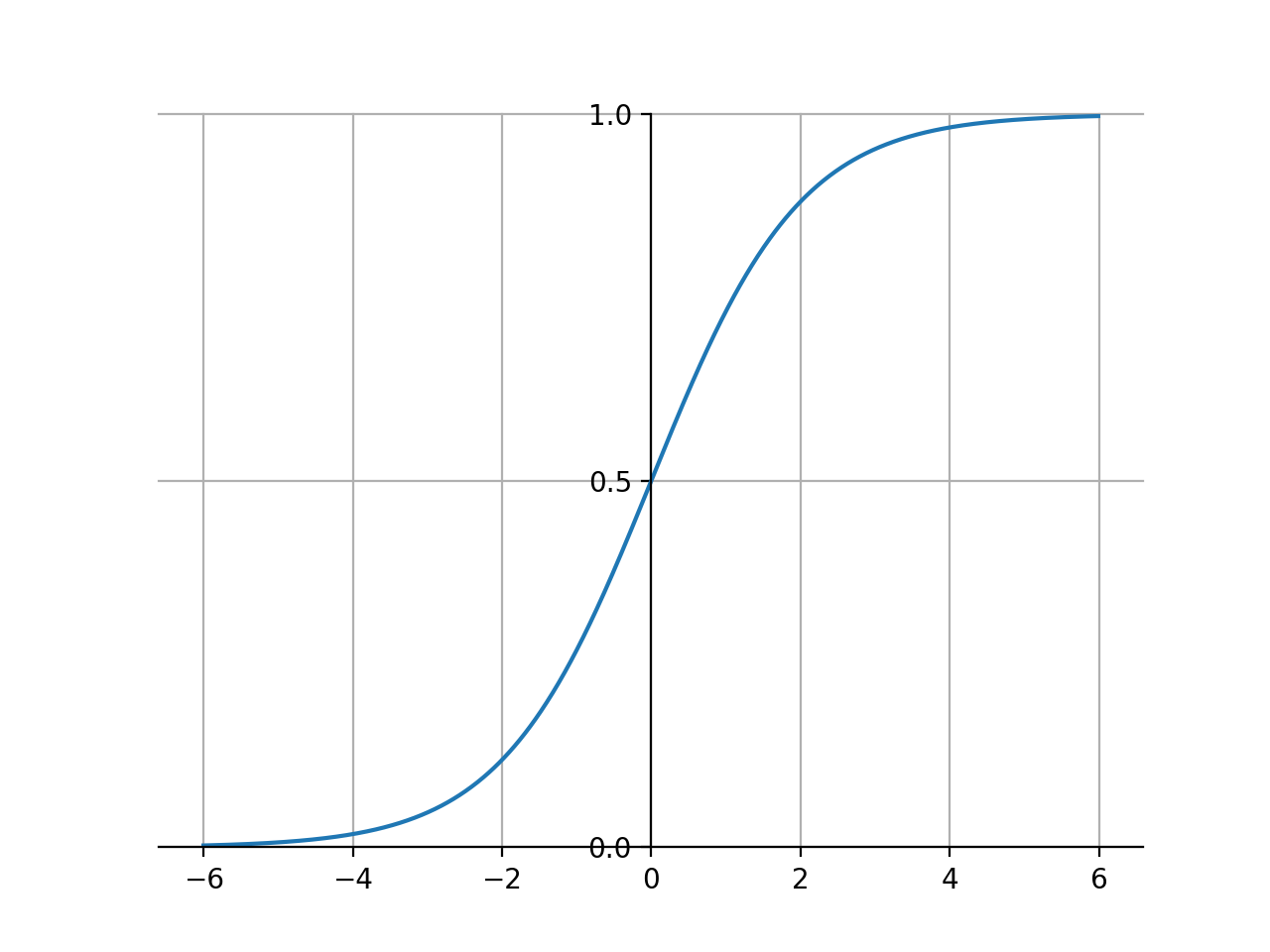
于是,我们令 (z= heta^T x) 就可以得到逻辑回归的模型:
[h_{ heta}(x)=frac{1}{1+e^{- heta^T x}}
]
假设:
[egin{aligned}
P(y=1|x; heta) & = h_{ heta}(x) \
P(y=0|x; heta) & = 1- h_{ heta}(x)
end{aligned}
]
上面两个关于概率的公式如果用一个式子表示出来就是:
[P(y|x; heta)=(h_{ heta}(x))^{y}(1- h_{ heta}(x))^{1-y}
]
2. 模型参数估计
逻辑回归中,模型参数为( heta)。从似然函数或者损失函数的角度+梯度下降法,都可以推导,本文以极大似然估计法为例:
似然函数为:
[prod_{i=1}^{m}(h_{ heta}(x^{(i)}))^{y^{(i)}}(1- h_{ heta}(x^{(i)}))^{1-y^{(i)}}
]
取对数得到对数似然函数为:
[egin{aligned}
L( heta) &= sum_{i=1}^{m}[ y^{(i)}ln(h_{ heta}(x^{(i)})) + (1-y^{(i)})ln(1-h_{ heta}(x^{(i)})) ] \
& = sum_{i=1}^{m}[ y^{(i)}ln frac{h_{ heta}(x^{(i)})}{1-h_{ heta}(x^{(i)})} - ln(1-h_{ heta}(x^{(i)}))] \
& = sum_{i=1}^{m} [ y^{(i)} heta^T x - ln(1-h_{ heta}(x))]
end{aligned}
]
对( heta_j)求导,梯度等于:
[egin{aligned}
frac{partial L( heta)}{partial heta_j} &= sum_{i=1}^{m}(y^{(i)}x_j^{(i)} - h_{ heta}(x^{(i)})x_j^{(i)})\
&= sum_{i=1}^{m}(y^{(i)}-h_{ heta}(x^{(i)}))x_j^{(i)}
end{aligned}
]
梯度下降法:(这里要求极大值,所以其实是梯度“上升”)
对参数进行更新:
[ heta_j = heta_j + alpha*sum_{i=1}^{m}(y^{(i)}-h_{ heta}(x^{(i)}))x_j^{(i)}
]
上面的梯度需要用到所有样本值,是“批量”梯度下降,有时为了加快计算,用随机梯度下降:
[ heta_j = heta_j + alpha*(y^{(i)}-h_{ heta}(x^{(i)}))x_j^{(i)}
]