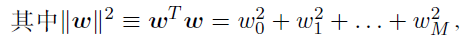知识要点:
1、通过多项式曲线拟合引出线性模型;
2、介绍多项式的阶数与模型复杂度的关系;
3、什么是过拟合、欠拟合;
4、解决过拟合、欠拟合的方法;
5、最小化误差平方和可以使用最大似然估计解释,并且过拟合问题是最大似然估计的一个必然结果。
读书笔记:

上图中N=10个蓝色样本点是函数sin(2*pi*x)加上一个随机噪声生成的样本点,曲线拟合的目标是在给定的10点的基础上,找出目标函数sin(2*pi*x),并且对给定一个新的输入x,预测对应的输出y。
使用如下(1-1)多项式函数来拟合样本点。

其中M是多项式的阶数(order),xj表示x的j次幂。多项式系数w0,w1,...,wM整体记作向量w。多项式函数y(x,w)是关于x的非线性函数,但是它是关于参数w线性的。类似这种关于未知参数的线性函数,称为线性模型。
定义误差平方和为损失函数:

目标是最小化(1.2)损失函数。该目标函数是关于w的二次函数,存在使得目标函数取得最小值的解w*。
其中多项式中的M是需要选择的一个超参数,它控制着模型的复杂度,M值过大,模型自由度越高,容易出现过拟合现象,相反M值过小则不能表达复杂的模型,最后建立的模型是欠拟合的。如下图表明了不同的M对样本点进行拟合的结果。

上图结果表明,M=1,2时对sin(2*pi*x)的拟合效果特别差,似乎当M=3的拟合效果是最好的,然后M=9的红色曲线虽然经过每一个样本点(10个样本点,w0,w1,..,w9十个自由度,一定可以经过所有样本点,根据范德蒙德行列式可以证明),但是范化能力差。
首先回到我们的目标:根据十个样本点,找出隐藏的函数sin(2*pi*x)后对新的样本数据进行预测。下面定量考查模型的范化能力与M的关系,假设我们有100个测试集数据用于模型范化能力的测试。定义均方根误差为:

其中N的样本个数,除以N是为了使得均方根误差和样本数量无关,开根是为了与目标变量t有相同的尺度。下图是不同M值在测试集上的均方根误差。

上图结果表明,过小的M在训练集上的误差较大,这可以归因于对应的多项式函数相当不灵活,不能够反映出sin(2pix)的震荡,当M=3,4,5,6,7,8时建立的模型范化能力都可以,但是当m=9时虽然在训练集上的误差为0,但是在测试集上的误差很大。
通过上图可知,对于简单的模型出现欠拟合问题,而过于复杂的模型则会出现过拟合现象,即模型被调节成与目标值的噪声想符号。
在本例中的欠拟合问题比较容易解决,可以增加模型的复杂度解决欠拟合问题;而对于过拟合问题则比较难解决。解决办法有:1、增加训练集数据规模。2、添加正则项。
方法一,增加训练集数据规模:如下图所示。
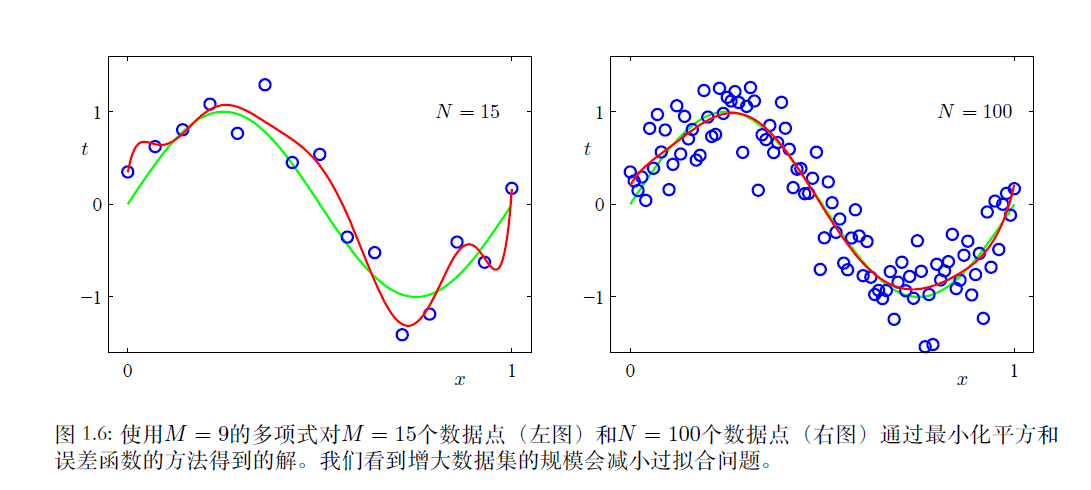
方法二:在损失函数中添加正则项是解决过拟合问题的另一种方法,具体公式1.4所示。