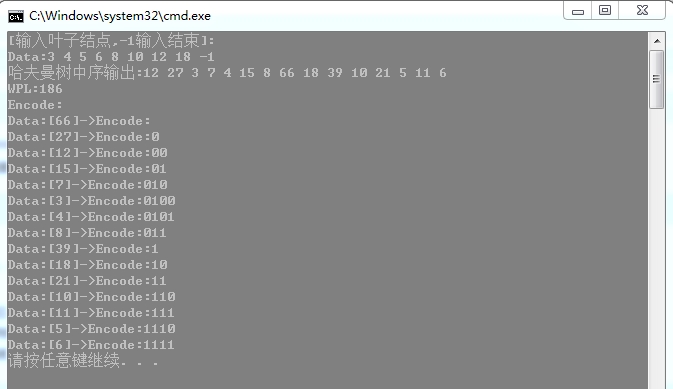
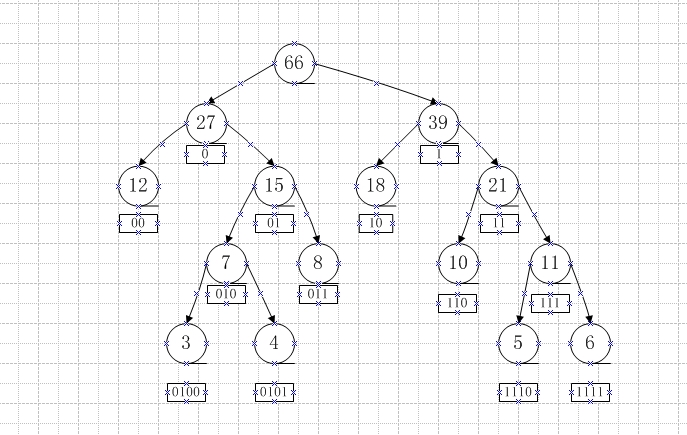
1 #include "iostream" 2 #include "vector" 3 using namespace std; 4 5 const int maxlen = 100; 6 #define infinity 65535 7 8 struct bnode 9 { 10 int data;//数据 11 bnode *lchild,*rchild; 12 vector<int>encode; 13 bool flags;//使用标志 14 }; 15 16 bnode *tree[maxlen]; 17 18 void initialization(vector<int>A,bnode *tree[maxlen])//初始化 19 { 20 int i; 21 for(i=0;i<A.size();i++) 22 { 23 tree[i] = new bnode; 24 tree[i]->data = A[i];//结点的值 25 tree[i]->flags = true;//标识未使用 26 tree[i]->lchild = NULL;//左子树为空 27 tree[i]->rchild = NULL;//右子树为空 28 } 29 } 30 31 void merge(int &n,bnode *tree[maxlen])//寻找当前根结点值最小的两个子树将其合并 32 { 33 int i,num1,num2,min1,min2; 34 min1 = infinity; 35 min2 = infinity; 36 for(i=0;i<n;i++)//寻找当前值最小的根节点 37 { 38 if((tree[i]->data<min1)&&tree[i]->flags) 39 { 40 min1 = tree[i]->data; 41 num1 = i; 42 } 43 } 44 tree[num1]->flags = false;//设置标识已使用过 45 46 for(i=0;i<n;i++)//寻找当前值最小的根节点 47 { 48 if((tree[i]->data<min2)&&tree[i]->flags) 49 { 50 min2 = tree[i]->data; 51 num2 = i; 52 } 53 } 54 tree[num2]->flags = false;//设置标识已使用过 55 //将两个子树合并 56 tree[n] = new bnode; 57 tree[n]->data = tree[num1]->data + tree[num2]->data; 58 tree[n]->flags = true; 59 tree[n]->lchild = tree[num1]; 60 tree[n]->rchild = tree[num2]; 61 n++; 62 } 63 64 void Huffmantree(int &n,bnode *tree[maxlen])//构造哈夫曼树 65 { 66 int i,num; 67 bool flags = true;//标识 68 while(flags) 69 { 70 num = 0;//计数 71 for(i=0;i<n;i++)//统计未使用结点数 72 { 73 if(tree[i]->flags) 74 { 75 num++; 76 } 77 } 78 if(num>=2) 79 { 80 merge(n,tree);//合并当前根结点值最小的两棵子树 81 }else{ 82 flags = false;//哈夫曼树构造完成标识 83 } 84 } 85 } 86 87 void HFTree(bnode *Tree)//中序输出哈夫曼树 88 { 89 if(Tree) 90 { 91 HFTree(Tree->lchild); 92 cout<<Tree->data<<" "; 93 HFTree(Tree->rchild); 94 } 95 } 96 97 void WPL(bnode *Tree,int &wpl)//求带权路径长度 98 { 99 if(Tree) 100 { 101 if(Tree->lchild&&Tree->rchild) 102 { 103 wpl+=Tree->data; 104 } 105 WPL(Tree->lchild,wpl); 106 WPL(Tree->rchild,wpl); 107 } 108 } 109 110 void Encode(bnode *Tree,bnode *root)//每个结点进行编码 111 { 112 int i; 113 if(Tree) 114 { 115 if(Tree->lchild)//左子树根结点添加0 116 { 117 for(i=0;i<Tree->encode.size();i++) 118 { 119 Tree->lchild->encode.push_back(Tree->encode[i]); 120 } 121 Tree->lchild->encode.push_back(0); 122 } 123 if(Tree->rchild)//右子树根结点添加1 124 { 125 for(i=0;i<Tree->encode.size();i++) 126 { 127 Tree->rchild->encode.push_back(Tree->encode[i]); 128 } 129 Tree->rchild->encode.push_back(1); 130 } 131 Encode(Tree->lchild,root);//左子树继续 132 Encode(Tree->rchild,root);//右子树继续 133 } 134 } 135 136 137 void print_Encode(bnode *Tree)//编码先序打印 138 { 139 int i; 140 if(Tree) 141 { 142 cout<<"Data:["<<Tree->data<<"]->Encode:"; 143 for(i=0;i<Tree->encode.size();i++) 144 { 145 cout<<Tree->encode[i]; 146 } 147 cout<<endl; 148 print_Encode(Tree->lchild); 149 print_Encode(Tree->rchild); 150 } 151 152 } 153 154 int main() 155 { 156 int x,n; 157 vector<int>Array; 158 cout<<"[输入叶子结点,-1输入结束]:"<<endl; 159 cout<<"Data:"; 160 cin>>x; 161 while(x!=-1) 162 { 163 Array.push_back(x); 164 cin>>x; 165 } 166 n = Array.size(); 167 initialization(Array,tree);//左右子树初始化 168 Huffmantree(n,tree);//构造哈夫曼树 169 cout<<"哈夫曼树中序输出:"; 170 HFTree(tree[n-1]); 171 cout<<endl; 172 173 int wpl = 0; 174 WPL(tree[n-1],wpl); 175 cout<<"WPL:"<<wpl<<endl; 176 cout<<"Encode:"<<endl; 177 Encode(tree[n-1],tree[n-1]); 178 print_Encode(tree[n-1]); 179 return 0; 180 }