王者之剑（最小割，最大独立集）

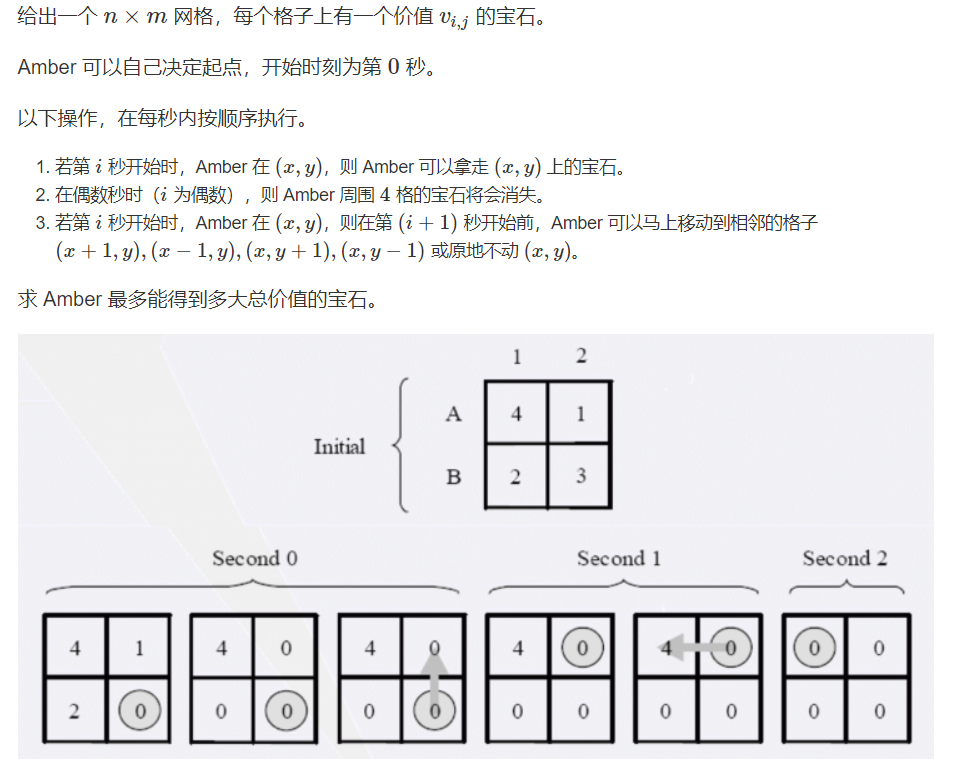
题意

思路

首先可以发现两个性质：

• 只有在偶数秒才可以拿宝石

• 相邻格子的宝石不能都拿到

根据这两条性质，可以发现这是一个二分图最大独立集问题。

对网格构建二分图，即横纵坐标之和为奇数的格点与源点(S)连容量是宝石价值的边，汇点(T)与横纵坐标之和为偶数的格点连容量是宝石价值的边。

横纵坐标之和为奇数的格点向上下左右四个格点，连容量是(infty)的边。

最大权独立集 = 总权值 - 最小权点覆盖

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 10010, M = 6 * N, inf = 1e8;

int n, m, S, T;
int h[N], e[M], ne[M], f[M], idx;
int cur[N], d[N];

int dx[4] = {-1, 1, 0, 0};
int dy[4] = {0, 0, -1, 1};

void add(int a, int b, int c)
{
    e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx ++;
    e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx ++;
}

bool bfs()
{
    memset(d, -1, sizeof(d));
    queue<int> que;
    que.push(S);
    d[S] = 0, cur[S] = h[S];
    while(que.size()) {
        int t = que.front();
        que.pop();
        for(int i = h[t]; ~i; i = ne[i]) {
            int ver = e[i];
            if(d[ver] == -1 && f[i]) {
                d[ver] = d[t] + 1;
                cur[ver] = h[ver];
                if(ver == T) return true;
                que.push(ver);
            }
        }
    }
    return false;
}

int find(int u, int limit)
{
    if(u == T) return limit;
    int flow = 0;
    for(int i = cur[u]; ~i && flow < limit; i = ne[i]) {
        cur[u] = i;
        int ver = e[i];
        if(d[ver] == d[u] + 1 && f[i]) {
            int t = find(ver, min(f[i], limit - flow));
            if(!t) d[ver] = -1;
            f[i] -= t, f[i ^ 1] += t, flow += t;
        }
    }
    return flow;
}

int dinic()
{
    int res = 0, flow;
    while(bfs()) {
        while(flow = find(S, inf)) {
            res += flow;
        }
    }
    return res;
}

int get(int x, int y)
{
    return (x - 1) * m + y;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof(h));
    S = 0, T = N - 1;
    int tot = 0;
    for(int i = 1; i <= n; i ++) {
        for(int j = 1; j <= m; j ++) {
            int x;
            scanf("%d", &x);
            int t = get(i, j);
            if((i + j) % 2) add(S, t, x);
            else add(t, T, x);
            tot += x;
        }
    }
    for(int i = 1; i <= n; i ++) {
        for(int j = 1; j <= m; j ++) {
            int t = get(i, j);
            if((i + j) % 2) {
                for(int k = 0; k < 4; k ++) {
                    int x = i + dx[k], y = j + dy[k];
                    if(x < 1 || x > n || y < 1 || y > m) continue;
                    int p = get(x, y);
                    add(t, p, inf);
                }
            }
        }
    }
    printf("%d
", tot - dinic());
    return 0;
}