第五讲.矩阵的逆

矩阵可逆的性质

1. 若方阵(A)满足(AB = I, CA = I)，则(B = C)。特别地，方阵的逆唯一。

证明：(C = CI = C(AB) = (CA)B = IB = B)

2. 若(A)可逆，则(Ax = b)有唯一解(x = A^{-1}b)

证明：(Ax = b)两边同时左乘(A^{-1})得：(x = A^{-1}Ax = A^{-1}b)

3. (Ax = 0)有非零解(Longrightarrow)(A)不可逆

4. (2 imes 2)矩阵(pmatrix{a & b\ c & d})可逆(Leftrightarrow)(ad - bc eq 0)，且(A^{-1} = frac{1}{ad - bc}pmatrix{d & -b\ -c & a})

5. 对角矩阵(D = pmatrix{d_1 & &\ & ddots & \ & & d_n})可逆(Leftrightarrow)(d_i eq 0(1 leq i leq n))，且(D^{-1} = pmatrix{1/d_1 & &\ & ddots & \ & & 1/d_n})

6. 若方阵(A, B)满足(AB = I)，则(BA = I)，且(A^{-1} = B)

定理：

1. 若(A)是可逆矩阵，则 (A^{-1})也可逆，且((A^{-1})^{-1} = A)
2. 若(n)阶方阵(A)和(B)都可逆,则(AB)可逆，且((AB)^{-1} = B^{-1}A^{-1})
3. 若(A)可逆，则(A^T)也可逆，且((A^T)^{-1} = (A^{-1})^T)

Gauss-Jordan消元法求逆

(E[A, I] = [I, A^{-1}])
例：

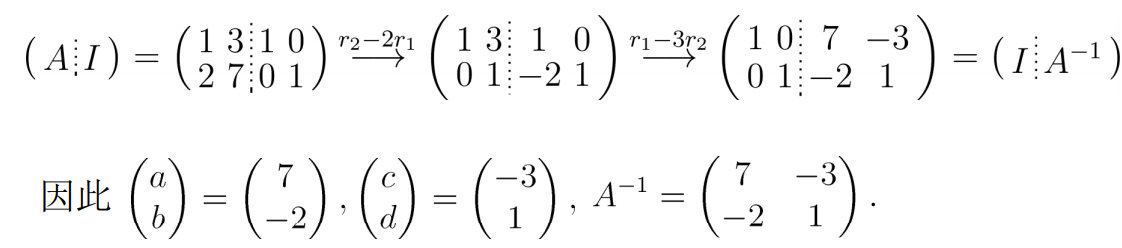
定理：(n)阶矩阵(A)可逆(Leftrightarrow)(A)有(n)个主元。

证明：“(Leftarrow)”若(n)阶方阵(A)有(n)个主元，则方程组(Ax = e_i(1 leq i leq n))有唯一解(x_1, dots, x_n)。则(A(x_1, dots, x_n) = I)，得(A)的右逆。此时，(A)可经过一系列初等行变换化为单位矩阵,，即存在初等矩阵(E_1, E_2, dots, E_k)，使得(E_kdots E_1A = I)，于是得(A)的左逆。对方阵(A)右逆(=)左逆(=)逆, 故(A)可逆。

“(Rightarrow)”设(A)可逆，即存在矩阵(B)，使(AB = BA = I)。假设(A)没有(n)个主元，则对(A)用初等行变换必产生至少一个零行，即存在初等矩阵的乘积(E)使(EA)有零行。于是((EA)B = E(AB) = E)也有零行，这与(E)是初等矩阵的乘积矛盾。因此(n)阶可逆方阵(A)必有(n)个主元。

下三角矩阵的逆

定理：两个(n)阶下(上)三角矩阵(A)与(B)的乘积仍为下(上)三角矩阵, 且(AB)的主对角元等于(A)与(B)的相应主对角元的乘积。

定理：下三角矩阵可逆(Leftrightarrow)主对角元素都非零。可逆下三角矩阵的逆也是下三角阵。若原矩阵对角元素都是(1)则逆的对角元也都是(1)。

分块矩阵

例：设(A = pmatrix{A_{11} & A_{12} \ 0 & A_{22}})为可逆的分块上三角矩阵，其中(A_{11})是(p imes p)矩阵，(A_{22})为(q imes q)矩阵，求(A^{-1})

解：用(B)表示(A^{-1})且把它分块使(pmatrix{A_{11} & A_{12} \ 0 & A_{22}}pmatrix{B_{11} & B_{12} \ B_{21} & B_{22}} = pmatrix{I_p & 0 \ 0 & I_q})。故有：

(A_{11}B_{11} + A_{12}B_{21} = I_p, A_{11}B_{12} + A_{12}B_{22} = 0, A_{22}B_{21} = 0, A_{22}B_{22} = I_q)

由此解得(B_{22} = A_{22}^{-1}, B_{21} = 0, B_{11} = A_{11}^{-1}, B_{12} = -A_{11}^{-1}A_{12}A_{22}^{-1})

于是(A^{-1} = pmatrix{A_{11}^{-1} & -A_{11}^{-1}A_{12}A_{22}^{-1} \ 0 & A_{22}^{-1}})