
真的是超级简单的一次信心赛,但我还是爆炸……
T1:秒切
T2:秒切
T3:这题意是啥???
明天中午有直播讲解。到时候再把不会的题改了。
11.10 20:37 upd:这个讲评,它Error了
已更新T3正解
T1:
入门难度。
一条n个节点的链,你可以跳过其中k段,求从1到n的最小长度。
贪心跳最大即可。暴力能过。
扫一遍,维护一个当前k段长度和总长度和,当前k段长度打擂台求最大,输出总长度减去最大k段长度。
(O(n))。
T2:
依旧入门难度。一段01序列,求有多少个连续(均为0或均为1)子串。
扫一遍判断当前值与上一个值是否相等即可。暴力能过。
(O(n))。
T3:

给定(S),(T)初始为空串,每次操作在(T)最前或最后插入一个字符,并求有多少个不同的(l),使得(l)范围内没有对应相同的元素。
(即$forall iin[1,~l],S[i] ot= T[T.size()-l+i] $)
17分:
考虑类似于最大公共子串的写法。
表格中的一个格子((x,~y))为true,当且仅当对应的(S[x])与(T[y])不同
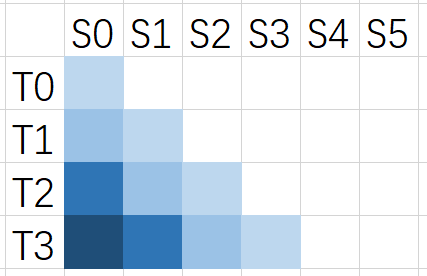
每次维护(T),并重新求一次(l)。
把每种相同颜色的方格称为一条对角线,由于只有(T)的尾部和(S)的头部能重合,合法的对角线只有上图中的几条。
每次扫一遍图中有几条对角线,线上所有格子均为true。
(O(m^3))。(大概吧)
50分:
由于每次只能(T)的首尾添加元素,考虑两种情况:
1.若在尾部添加:
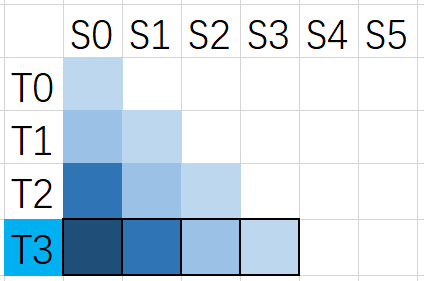
则只需要考虑黑色框起来的几个格子。
如果第一个格子((0,~3))为true,则ans++。
存储每条对角线是否成立(即均为true),如果其余几个格子所在的对角线成立,而这个格子不为true,则ans--。
2.若在头部添加:
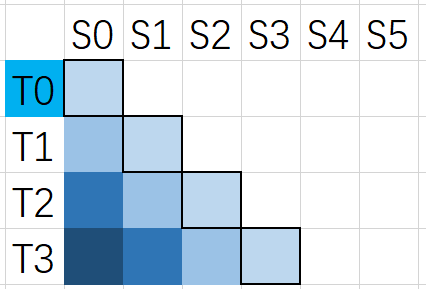
则需要增加一条新的对角线,跑一遍这个对角线是否成立。
总体(O(m^2))。大概吧。考场上就想到这。
貌似bitset优化后70pts,再开个O2就A了
100分:
每个位子和每种字符都是独立的,对每种字符都记录一下位子。
用(f[i]=0 ~or~ 1)表示长度为的(i)后缀可不可以,(0)表示可以,(1)表示不行。
考虑(f)只有(0)和(1),可以用bitset优化,对每种字符都开一个bitset记录是不是该字符。
在末尾加一个字符时,左移后做(or)运算。
在开头加一个字符时,直接(or)上该字符出现的状态左移长度减一位。
答案就是范围内(0)的个数。
复杂度(O(m^2/w))
大概来说就是不用真的维护一个(T),参考我之前画的那个表,由于只是比较字符是否不同,记录字符出现的位置即可。利用bitset的位运算优化速度。
反思:就算没有想到用bitset记录字符位置,存储那个对角线是否成立的bool数组由于需要两端插入,我用的是vector……对于bitset一类的还是不熟。考前还是要再看一下。
T4:
看上去就不太可做的一道多项式求和。
8分:
模拟题意。
16分:
加一个记忆化一类的优化。
100分:
不会。待更。
upd:题解它Error了