《极客时间--算法面试》--贪心算法

广度优先搜索算法，这个代码不仅适应于树也适应于图。图会有回路结构，需要判重，采用set去重。

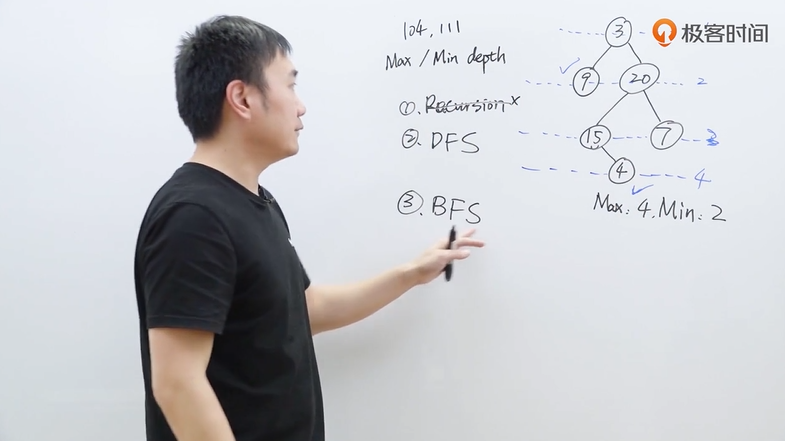
二叉树的最大104、最小深度111

思路：

　　一、采用递归的思路

　　二、采用BFS广度优先搜索

　　三、深度优先搜索

此图是广度优先搜索算法，一层一层去遍历，终点是找到叶子节点为止。

最开始的叶子节点是最小深度，最后到达的是最大深度。

此图是深度优先搜索的方法，每次遍历更新最大和最小。还是以判断叶子节点。

时间复杂度都为O(n)，因为总共有n个节点，都需要遍历一次，所以是O(n)

虽然推理是采用广度或者深度优先的策略，但是实际代码采用的是递归的思路写的。

二叉树的最大深度代码：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return 0                                                        #如果是叶子节点则返回0
        return 1+max(self.maxDepth(root.left),self.maxDepth(root.right))    #调用左子树和右子树，最大值加1

二叉树的最小深度代码：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:                                    #如果是空节点，直接返回0
            return 0
        if not root.left:                               #如果左子节点为空，那么去查找右子树的节点
            return 1+self.minDepth(root.right)
        elif not root.right:                            #同理，如果右子节点为空，那么去查找左子树的节点
            return 1+self.minDepth(root.left)
        else:                                           #否则，说明有左右子节点，左右子树的最小值加1
            return 1+min(self.minDepth(root.left),self.minDepth(root.right))
        

括号生成

https://leetcode-cn.com/problems/generate-parentheses/submissions/

思路：

　　我也没听懂，后期花点时间弄懂，暂记着。

　　

代码：

class Solution(object):
    def generateParenthesis(self, n):
        """
        :type n: int
        :rtype: List[str]
        """
        self.list = []
        self._gen(0,0,n,"")
        return self.list
    def _gen(self,left,right,n,result):
        if left==n and right==n:                            #左右括号已经配额完毕
            self.list.append(result)                        #将result加入到结果当中
            return 
        if left < n:
            self._gen(left+1,right,n,result+'(')            #加入左括号，随时都可以加进去，只要没有用完都可以
        if left>right and right<n:                          #右括号个数小于左括号并且右括号没有用完
            self._gen(left,right+1,n,result+')')            #加入右括号